| Solved | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 8/10 | O | . | O | O | O | O | O | Ø | . | Ø |
- O for passing during the contest
- Ø for passing after the contest
- ! for attempted but failed
- · for having not attempted yet
A
题目描述
有$n(2\leq n\leq 1000)$个气球,分别有$h_i$的高度,给定$h_i+h_j=a_{ij}$的矩阵$A$,求$h$。保证答案唯一。
解题思路
$n\geq 3$的时候,联立三个方程求解$h_1$,再求其他解。$n=2$时因为答案唯一,输出$\text{1 1}$。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
typedef long long ll;
using namespace std;
int h[N],a[N][N];
int main(){
int i,j,n;
scanf("%d",&n);
if(n==2)return printf("1 1"),0;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
h[1]=(a[1][3]+a[1][2]-a[2][3])/2;
for(i=2;i<=n;i++)h[i]=a[1][i]-h[1];
for(i=1;i<=n;i++)printf("%d ",h[i]);
return 0;
}
B
题目描述
解题思路
AC代码
2
C
题目描述
给定一个$n(1\leq n\leq 17)$点$m(1\leq m\leq 136)$边的无向图,现要对每个边定向,使之成为一个$DAG$并最小化最长路长度。求这个最小长度。
解题思路
染色,连边时从颜色编号小连向颜色编号大,故最长路为最少染色数$-1$。染色通过状压$DP$,枚举合法子集标记,然后枚举状态和状态的子集转移即可。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
typedef long long ll;
using namespace std;
int f[N],g[N];
int mt[20][20];
int main(){
int i,j,k,n,m;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);u--;v--;
mt[u][v]=mt[v][u]=1;
}
memset(g,0x3f,sizeof(g));
for(i=0;i<(1<<n);i++)
for(j=0;j<n;j++)
for(k=j+1;k<n;k++)
if((i&(1<<j))&&(i&(1<<k))&&mt[j][k])f[i]=1;
g[0]=0;
for(i=0;i<(1<<n);i++)
for(j=i;j;j=(j-1)&i)
if(!f[j])g[i]=min(g[i],g[i-j]+1);
printf("%d",g[(1<<n)-1]-1);
return 0;
}
D
题目描述
求$\sum_{i=1}^{n}f(i)$,其中$f(n)=\sum_{i=1}^{n}\sum_{j=1}^{n}gcd(i,j,n)$。
解题思路
每次遇到数论题都不太会推式子,这里非常详细地推一遍。
$f(n)$
$=\sum_{d|n}\sum_{i=1}^{n}\sum_{j=1}^{n}d[gcd(i,j,n)==d]$
$=\sum_{d|n}\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}d[gcd(i,j,\frac nd)==1]$
$=\sum_{d|n}\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}d\epsilon (gcd(i,j,\frac nd))$
$=\sum_{d|n}\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}d\sum_{e|(gcd(i,j,\frac nd))}\mu (e) $
$=\sum_{d|n}\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}d\sum_{e|i,e|j,e|\frac nd}\mu (e) $
上式有条件:$e|i,e|j,de|n,d|n$等价于:$e|i,e|j,e|n,de|n$
$=\sum_{e|n}\mu(e)\sum_{d|\frac ne}d\sum_{i=1}^{\frac nd}\sum_{j=1}^{\frac nd}[e|i,e|j]$
$=\sum_{e|n}\mu(e)\sum_{d|\frac ne}d\sum_{i=1}^{\frac n{de}}\sum_{j=1}^{\frac n{de}}1$
$=\sum_{e|n}\mu(e)\sum_{d|\frac ne}d(\frac n{de})^2$
设$x=de$,条件$e|n,ed|n$变为$x|n,d|x$
$=\sum_{x|n}\sum_{d|x}(\frac nx)^2d\mu(\frac xd)$
$\mu\times id=\phi$
$=\sum_{x|n}(\frac nx)^2\phi(x)$
$=\sum_{x|n}x^2\phi(\frac nx)$
于是
$\sum_{i=1}^{n}f(i)$
$=\sum_{i=1}^{n}\sum_{x|i}x^2\phi(\frac ix)$
$i=xk$
$=\sum_{x=1}^{n}x^2\sum_{k=1}^{\lfloor\frac nx\rfloor}\phi(\frac{xk}x)$
$=\sum_{x=1}^{n}x^2\sum_{k=1}^{\lfloor\frac nx\rfloor}\phi(k)$
欧拉函数前缀和可以杜教筛,外层数论分块。
缺失知识点:
$\mu\times I=\epsilon, \phi\times I=id,\mu\times id=\phi$
另外,此题需要注意$mod$是质数,但不一定不是$2,3$,故在计算时需要避免使用逆元。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
typedef long long ll;
using namespace std;
int pri[N],phi[N],cnt,isnp[N];
int mod,n;
void sieve(){
int i,j;
isnp[0]=isnp[1]=1;
phi[1]=1;
for(i=2;i<N;i++){
if(!isnp[i])pri[cnt++]=i,phi[i]=i-1;
for(j=0;j<cnt;j++){
if(1LL*i*pri[j]>=N)break;
isnp[i*pri[j]]=1;
if(i%pri[j])phi[i*pri[j]]=phi[i]*(pri[j]-1)%mod;
else{
phi[i*pri[j]]=phi[i]*pri[j]%mod;
break;
}
}
}
//for(i=1;i<100;i++)printf("%d ",phi[i]);
for(i=2;i<N;i++)(phi[i]+=phi[i-1])%=mod;
}
unordered_map<int,ll>ansphi;
inline ll getsphi(ll n){//S=sum of f
if(n<N)return phi[n];
if(ansphi[n])return ansphi[n];
ll ans=(n*(n+1))/2%mod;
register unsigned int l,r;//sum of f*g
for(l=2;l<=n;l=r+1){
r=n/(n/l);
(ans-=(r-l+1)*getsphi(n/l))%=mod;//sum of g(r-l),times S(n/l)
}
return ansphi[n]=(ans%mod+mod)%mod;
}
ll getsq(ll x){//x(x+1)(2x+1)/6
ll t=x*(x+1)/2;
if(t%3)return (2*x+1)/3*(t%mod)%mod;
else return t/3%mod*(2*x%mod+1)%mod;
}
int main(){
int i,r;
ll ans=0;
scanf("%d%d",&n,&mod);
sieve();
for(i=1;i<=n;i=r+1){
r=n/(n/i);
(ans+=(getsq(r)-getsq(i-1))*getsphi(n/i))%=mod;
}
printf("%lld",(ans+mod)%mod);
return 0;
}
E
题目描述
两个人在下棋,都想让先手赢。棋盘是$n\times m$的黑白棋盘,每次可以翻转从左上角到任意点之间的矩形内的黑白情况,谁把棋盘全变白谁就赢,问先手能否赢。
解题思路
两人都想让先手赢,所以除了左上角的格子都是可以控制黑白颜色的,但由于每回合左上角都会被翻一次,所以如果左上角是白色那么必输,否则必赢。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
typedef long long ll;
using namespace std;
char a[520][520];
int main(){
int i,t,n,m;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)scanf("%s",a[i]);
printf("%s\n",a[0][0]=='1'?"call":"aoligei");
}
return 0;
}
F
题目描述
给定一个数组$a$,求切成$k$段(每段非空),使得每段$[l_i,r_i]$内相同数对($a_i=a_j,i\neq j,i,j\in[l_k,r_k]$)的数量之和最小,求这个最小值。
解题思路
有显然$DP$:设$f[i][j]$表示到第$i$个元素,一共已经分成了$j$段的最小值。
$f[i][j]=min_{k<i}(f[k][j-1]+cost(k,i))$,其中$cost(k,i)$表示$[k+1,i]$区间内数组$a$的相同数对个数。
固定第二维,显然有决策单调性。因为决策单调性优化$DP$的区间改动范围较小,$cost$用莫队即可求解。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
typedef long long ll;
using namespace std;
ll f[N][22];
int n,k,a[N];
int buc[N],pL,pR;
ll AA;
void upd(int x,ll f){AA+=f*(buc[x]-1ll)*buc[x]/2;}
ll calc(int l,int r){
while(pL<l){
upd(a[pL],-1);buc[a[pL]]--;
upd(a[pL],1);pL++;
}
while(r<pR){
upd(a[pR],-1);buc[a[pR]]--;
upd(a[pR],1);pR--;
}
while(l<pL){
pL--;
upd(a[pL],-1);buc[a[pL]]++;
upd(a[pL],1);
}
while(pR<r){
pR++;
upd(a[pR],-1);buc[a[pR]]++;
upd(a[pR],1);
}
return AA;
}
void solve(int l,int r,int pl,int pr,int now){//qiu f[mid]=f[p]...?
if(l>r||pl>pr)return;
int mid=(l+r)/2,nxt=0;
for(int i=pl;i<=pr;i++){
ll tmp=calc(i+1,mid);//md
if(f[i][now-1]+tmp<f[mid][now])f[mid][now]=tmp+f[i][now-1],nxt=i;
}
solve(l,mid-1,pl,nxt,now);
solve(mid+1,r,nxt,pr,now);
}
int main(){
int i,j;
memset(f,0x3f,sizeof(f));
f[0][0]=0;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
pL=pR=1;buc[a[1]]++;
for(i=1;i<=k;i++)solve(1,n,0,n-1,i);
printf("%lld",f[n][k]);
return 0;
}
G
题目描述
给一棵$n$顶点的有权树,其中$k$个顶点为关键点。计算出$i(1\leq i\leq n)$为根节点时,遍历到所有关键点所需最少总权值。
解题思路
答案显然为($i$和关键点组成的生成树内权值之和)$*2-$距离$i$最远的关键点的距离。
树形$DP$求解,先解出$1$为根时,所有点对应子树有多少个关键点$sz[p]$,以及生成树内权值之和$sts[p]$($\text{spanning tree sum}$),这样可以很容易通过换根时讨论子树大小求出每个点的$sts[p]$。
距离$p$最远的关键点距离:$md[p]=max(fadis[p],sondis[p])$,$sondis$可以通过预处理$DP$出。而$fadis$在$p$不是$fa[p]$的最远点对应节点时,为$max(fadis[fa[p]],sondis[fa[p]])+len(p,fa[p])$,否则为$max(fadis[fa[p]],\text{2nd}sondis[fa[p]])+len(p,fa[p])$,故需要再维护一下次大距离和最大距离对应的节点。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
typedef long long ll;
using namespace std;
int hd[N],cnt;
struct Edge{
int e,n,l;
}e[N<<1];
int n,k,x,key[N];
void add(int a,int b,int l){e[++cnt].e=b;e[cnt].n=hd[a];hd[a]=cnt;e[cnt].l=l;}
ll sd[N],fd[N],md[N],sdd[N],son[N],sz[N],sts[N];
void dfs4dis(int p,int f){
int i;
sd[p]=sdd[p]=-1e16;son[p]=sz[p]=0;
if(key[p])sz[p]=1,sd[p]=0,son[p]=p;//我 是 我 儿 子
for(i=hd[p];i;i=e[i].n){
int q=e[i].e;
if(q==f)continue;
dfs4dis(q,p);
if(sz[q])sts[x]+=e[i].l,sz[p]+=sz[q];
if(sd[q]+e[i].l>sd[p]){
sdd[p]=sd[p];
sd[p]=sd[q]+e[i].l;
son[p]=q;
}else if(sd[q]+e[i].l>sdd[p])sdd[p]=sd[q]+e[i].l;
}
}
void dfs4sts(int p,int f){
int i;
for(i=hd[p];i;i=e[i].n){
int q=e[i].e;
if(q==f)continue;
if(sz[q]==k)sts[q]=sts[p]-e[i].l;
else if(sz[q])sts[q]=sts[p];
else sts[q]=sts[p]+e[i].l;
dfs4sts(q,p);
}
}
void dfs4md(int p,int f){
int i;
md[p]=max(fd[p],sd[p]);
for(i=hd[p];i;i=e[i].n){
int q=e[i].e;
if(q==f)continue;
if(q==son[p])fd[q]=max(fd[p],sdd[p])+e[i].l;
else fd[q]=max(fd[p],sd[p])+e[i].l;
dfs4md(q,p);
}
}
int main(){
int i;
scanf("%d%d",&n,&k);
for(i=1;i<n;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
while(k--)scanf("%d",&x),key[x]=1;
dfs4dis(x,0);
dfs4sts(x,0);
dfs4md(x,0);
for(i=1;i<=n;i++)printf("%lld\n",2*sts[i]-md[i]);
return 0;
}
H
题目描述
给一个长度为$n$的序列$a$,序列中的数互不相同。定义$g(x,y)$为序列删去了$[x,y]$区间之后的最大的$gcd$值,定义当删到只剩下$\leq 1$个元素时,$g(x,y)=0$。求$\sum_{i=1}^{n}\sum_{j=i}^{n}g(i,j)$。
解题思路
从大到小枚举$\gcd$为$g$的时候对答案的贡献。找到序列中$g$的倍数的下标,组成递增序列$v_1,v_2,…,v_k$,如果有这些数里的至少两个没被删掉,那么剩余区间的$\gcd$必然$\geq g$。
不妨先假设现在枚举的是最大的$\gcd$,即剩余区间的$\gcd=g$。
设$R[i]$表示以$i$为左端点、右端最大能删到哪里能够使剩余区间$\gcd=g$,那么必然有
$i\in[1,v_1],R[i]=max(R[i],v_{k-1}-1)$
$i\in [v_1+1,v_2],R[i]=max(R[i],v_k-1)$
$i\in [v2+1,n],R[i]=max(R[i],n)$
初始化$R[i]=i-1$。
于是每次进行这样的操作,计算出两次操作间相差了多少个区间,计算求和即可。
这种操作需要:区间置$max$;区间求和。
好,学到一手神秘还复杂度正确的操作。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
typedef long long ll;
using namespace std;
int a[N],pos[N];
ll sum[N<<2];
int lazy[N<<2],mn[N<<2],se[N<<2],cnt[N<<2],L[N<<2],R[N<<2];
vector<int>v[N];
void pushup(int p){
if(ls==rs)return;
sum[p]=sum[ls]+sum[rs];
if(mn[ls]==mn[rs]){
mn[p]=mn[ls];
se[p]=min(se[ls],se[rs]);
cnt[p]=cnt[ls]+cnt[rs];
}else if(mn[ls]<mn[rs]){
mn[p]=mn[ls];
se[p]=min(mn[rs],se[ls]);
cnt[p]=cnt[ls];
}else{
mn[p]=mn[rs];
se[p]=min(mn[ls],se[rs]);
cnt[p]=cnt[rs];
}
}
void puttag(int p,int tag){//set min to tag
if(mn[p]>=tag)return;
sum[p]+=1LL*(tag-mn[p])*cnt[p];
mn[p]=lazy[p]=tag;
}
void pushdown(int p){
if(lazy[p]==-1)return;
puttag(ls,lazy[p]);
puttag(rs,lazy[p]);
lazy[p]=-1;
}
void build(int p,int l,int r){
lazy[p]=-1;
L[p]=l;R[p]=r;
if(l==r){
mn[p]=sum[p]=l-1;
se[p]=1e9;
cnt[p]=1;
return;
}
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void modify(int p,int l,int r,int x){
if(L[p]>r||R[p]<l)return;
if(mn[p]>=x)return;
if(l<=L[p]&&R[p]<=r&&se[p]>=x){
puttag(p,x);
return;
}
pushdown(p);
modify(p<<1,l,r,x);
modify(p<<1|1,l,r,x);
pushup(p);
}
int main(){
int i,j,t,n,g;
scanf("%d",&t);
while(t--){
ll ans=0;
memset(pos,0,sizeof(pos));
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]),pos[a[i]]=i;
build(1,1,n);
for(i=1;i<N;i++){
v[i].clear();
for(j=i;j<N;j+=i)if(pos[j])v[i].push_back(pos[j]);
sort(v[i].begin(),v[i].end());
}
for(g=N-1;g;g--){
ll lastsum=sum[1];
if(v[g].size()<2)continue;
int l1=v[g][0],l2=v[g][1],r1=v[g][v[g].size()-2],r2=v[g][v[g].size()-1];
modify(1,1,l1,r1-1);
modify(1,l1+1,l2,r2-1);
modify(1,l2+1,n,n);
ans+=1LL*g*(sum[1]-lastsum);
}
printf("%lld\n",ans);
}
return 0;
}
I
题目描述
解题思路
AC代码
2
J
题目描述
对于字符串$s$和整数$k$,定义$f(s,k)$为,将$s$划分为至多$k$段$u_1,u_2,…,u_l$,最小化$max_{1\leq i\leq l}u_i$,求最小化的结果。
现在我们有一个字符串$S$,$q$次询问$f(s[l_i…|s|],k_i)$的值,每次询问输出一个区间$(a_i,b_i)$,表示$S[a_i…b_i]$。如果$a_i$有多个,输出$a_i$最小的解,要求$a_i\geq l_i$。
解题思路
先学一手$Lyndon$分解:
定义一个串为$Lyndon$串,当且仅当这个字符串的所有后缀中字典序最小的是字符串本身。
对一个字符串$s$的$Lyndon$分解是存在且唯一的。
假设$s=s_1s_2s_3…s_k$,其中$s_i$为$Lyndon$串,且有$s_i\geq s_{i+1}$。
Lyndon分解(Duval算法)模板代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
typedef long long ll;
using namespace std;
char s[2000010];
int main(){
int i,j,k,l;
scanf("%s",s+1);
l=strlen(s+1);
for(i=1;i<=l;){
j=i,k=i+1;
while(k<=l&&s[k]>=s[j]){
if(s[k]>s[j])j=i;
else j++;
k++;
}
while(i<=j){
printf("%d ",i+k-j-1);//每个lyndon串起始位置
i+=k-j;
}
}
return 0;
}
$Lyndon$分解还可以直接利用$Lyndon$串的性质(本身为最小的后缀),用后缀数组+单调栈求解。
对于本题,需要使用这种方法,因为需要知道以每个点开始的$Lyndon$串位置,且后面还需要用到$LCP$。
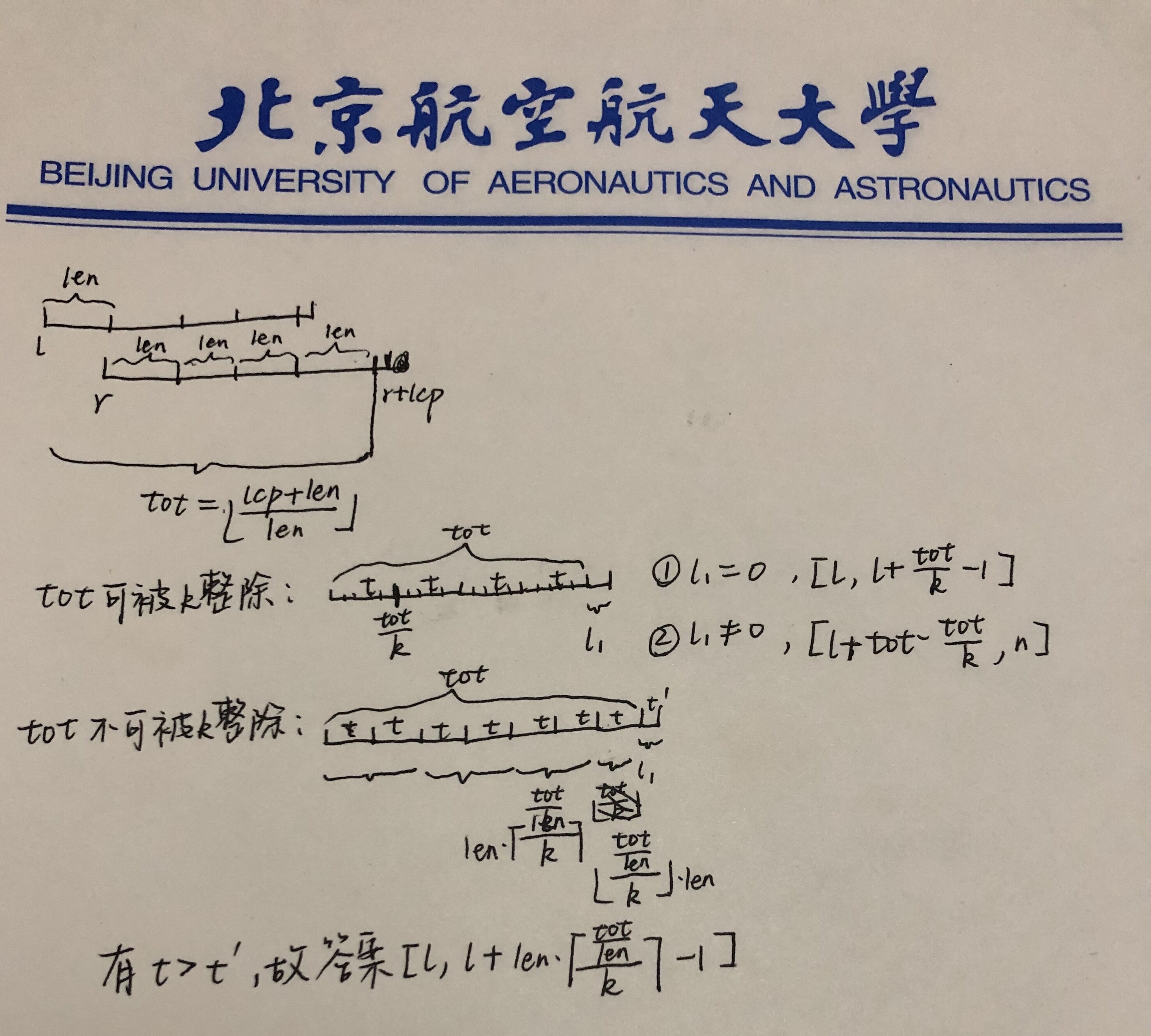
先找出$Lyndon$分解中$l$对应的下一个$Lyndon$串起始位置$r$,如果$lcp(suf(l),suf(r))=0$那么由$Lyndon$串性质,显然答案为$l,r-1$;否则中间可能会有一堆循环节,分类讨论循环节的个数能否整除、循环是否倒字符串结尾等即可。
具体讨论过程见图片:
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
typedef long long ll;
using namespace std;
char s[N];
int n,sa[N],c[N],x[N],y[N];
void getsa(int m){
int i,k;
for(i=0;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[x[i]=s[i]]++;//also x[i]=s[i]-'a'
for(i=1;i<=m;i++)c[i]+=c[i-1];
for(i=n;i;i--)sa[c[x[i]]--]=i;
for(k=1;k<=n;k<<=1){
int p=0;
for(i=n-k+1;i<=n;i++)y[++p]=i;
for(i=1;i<=n;i++)if(sa[i]>k)y[++p]=sa[i]-k;
for(i=0;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[x[y[i]]]++;
for(i=1;i<=m;i++)c[i]+=c[i-1];
for(i=n;i;i--)sa[c[x[y[i]]]--]=y[i];
swap(x,y);
p=x[sa[1]]=1;
for(i=2;i<=n;i++)
x[sa[i]]=y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]?p:++p;
if(p>=n)break;
m=p;
}
}
int h[N],rnk[N];
void geth(){
int i,j,k=0;
for(i=1;i<=n;i++)rnk[sa[i]]=i;
for(i=1;i<=n;i++){
if(k)k--;
j=sa[rnk[i]-1];
while(s[i+k]==s[j+k])k++;
h[rnk[i]]=k;
}
}
int rmq[N][22],lg[N];
void initlcp(){
int i,j;
for(i=2;i<N;i++)lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);
getsa(260);
geth();
for(i=1;i<=n;i++)rmq[i][0]=h[i];
for(i=1;i<=22;i++)
for(j=1;j+(1<<i-1)<=n;j++)
rmq[j][i]=min(rmq[j][i-1],rmq[j+(1<<i-1)][i-1]);
}
int getlcp(int x,int y){
if(x==y)return n-x+1;
if(rnk[x]>rnk[y])swap(x,y);
int l=rnk[x]+1,r=rnk[y];
int p=lg[r-l+1];
return min(rmq[l][p],rmq[r-(1<<p)+1][p]);
}
int sta[N],top,nxt[N];
int main(){
int i,q;
scanf("%s%d",s+1,&q);
n=strlen(s+1);
initlcp();
sta[top++]=n+1;
for(i=n;i;i--){
while(rnk[sta[top-1]]>rnk[i])top--;
nxt[i]=sta[top-1];
sta[top++]=i;
}
while(q--){
int r,l,k;
scanf("%d%d",&l,&k);
r=nxt[l];
if(k==1||r==n+1)printf("%d %d\n",l,n);
else{
int lcp=getlcp(l,r);
if(lcp==0)printf("%d %d\n",l,r-1);
else{
int len=r-l,tot=lcp/len*len+len;
if((tot/len)%k==0){
if(l+tot==n+1)printf("%d %d\n",l,l+tot/k-1);
else printf("%d %d\n",l+tot-tot/k,n);
}else printf("%d %d\n",l,l+((tot/len-1)/k+1)*len-1);
}
}
}
return 0;
}