从匈牙利算法到带权带花树——详解对偶问题在图匹配上的应用

发表于 | 评论数： | 阅读次数：

引入

前些天看到了一个比较有趣的题目，需要用到一般图最大权匹配。可是我只会二分图最大匹配，甚至不会 KM 和带花树的原理，于是就进行了一个资料的搜，顺便增长一下板子库。然而——

对一般图最大权匹配，网上现成高质量资料较少。

image-20210910094916403

苦于资料杂乱、且无论正确性还是代码具体实现都没有一个清晰的全流程教程，在吸取众长、奋斗三天后，终于通过了 UOJ 上的模板题。

image-20210910095208484

这篇博客主要目的在于，梳理整个流程（包含代码实现）中应用的原理和使用的技巧。一般图最大权匹配主要通过下面四个问题逐步转化：

  1. 二分图最大匹配
  2. 一般图最大匹配
  3. 二分图最大权匹配
  4. 一般图最大权匹配

本文主要描述，如何通过解决前三个问题的思路，解决第四个更为复杂的问题。本文的前置知识只有匈牙利算法。

基本定义

匹配：对于图 $G=(V,E)$ 的一个匹配 $M$ 是边集 $E$ 的子集，其中两两不共用顶点。

最大匹配：边数最多的匹配。

完美匹配：包含原图所有点的匹配。

最大权匹配：对于图 $G(V,E)$，边 $e\in E$ 的权重为 $w(e)$，最大权匹配 $M=(V’,E’)$ 为 $\sum_e w(e)$ 最大的匹配。

最大权最大匹配：最大权最大匹配 $M(V’,E’)$ 为 $\sum_e w(e)$ 最大的最大匹配。

匹配点、未匹配点、匹配边、非匹配边：字面含义，对应于某个匹配的状态。

交错路径：从一个未匹配点出发，依次交错经过非匹配边、匹配边形成的路径。

增广路：一个末尾是未匹配点的交错路径。这样的路径可以通过翻转整条路上边的选择状态获得一个长度恰好增加 $1$ 的匹配。

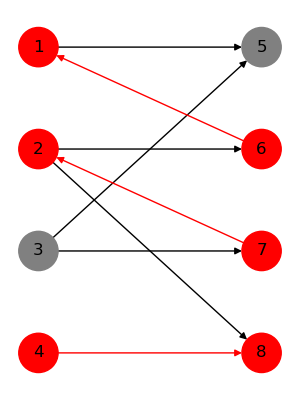
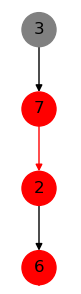
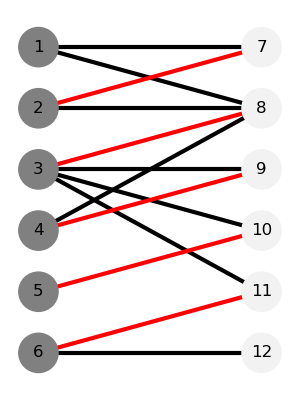
下列各图展示了一个无向二分图（箭头只是表示增广路的顺序）某时刻对增广路增广的情况。
二分图
一条交错路
一条增广路
对增广路增广

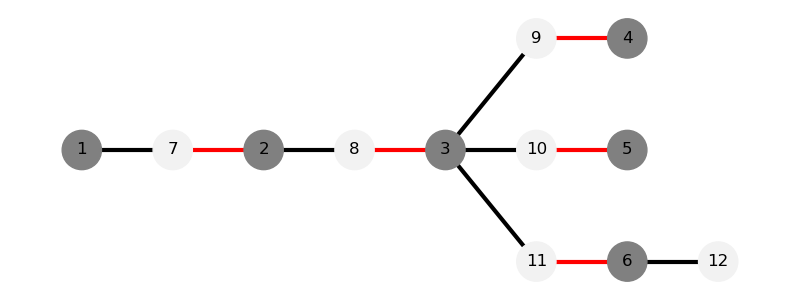
交错树：从未匹配点 $r$ 开始寻找增广路时，交错路径组成的树。其中，我们称向根方向匹配的点为 $S$ 点（黑点，偶点），背向根方向匹配的点为 $T$ 点（白点，奇点）。
二分图
以 1 为根的交错树

二分图最大匹配

二分图匹配可以用网络流做，Dinic 在二分图上的复杂度和 Hopcroft-Karp 相同，均为 $O(E\sqrt{V})$ ，不赘述。

匈牙利算法流传较广的是 DFS 做法，即枚举左部每个未匹配点，记录右部节点匹配的左部标号 $match_q$，检查交错路是否为增广路，复杂度 $O(VE)$。正确性是通过 Berge’s Theorm （如果找不到某点为端点的增广路，则最大匹配可以不包括这个点）证明的，比较显然。

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int dfs(int p,int t){ // p: 左半边编号 
    for(auto q:G[p])
        if(t!=vis[q]){
            vis[q]=t;
            if(match[q]==-1||dfs(mt[q],t))
                return match[q]=p,1;
        }
    return 0;
}
int maxmatch(){
    int ans=0;
    memset(match,-1,sizeof(match));
    for(int i=1;i<=n;i++)
        if(match[i]==-1&&dfs(i,i))ans++;
    return ans;
}

同样地，可以进行 BFS，即初始时所有点都未匹配，将未匹配点入队。逐个取出队首元素作为交错树的根，对交错树进行 BFS 匹配。可以看出，增广的本质是在以每个点为根的交错树上寻找增广路。而二分图左部永远是黑点，右部永远是白点，因此增广路的首末必分别在左部和右部。

一般图最大匹配

对于一般图，就没有这么好的性质了。但唯一的不同是，一般图中可能有奇数长度的环，下简称奇环。在奇环上的每一个点连出去的非匹配边，都能够成为某个增广路上的边，这导致在增广的过程中难以判断如何翻转。
增广路经过奇环的两种形式
我们发现，奇环具有了所有黑点需要具备的性质：任意点连出去的非匹配边都可以在从根开始的交错路上；奇环的根向根方向匹配。于是，将奇环缩成一个点，称为**花**。奇环的**根**，也就是整个环中唯一连了两个环内非匹配边的点，称为**花托**（上图中的 root）。

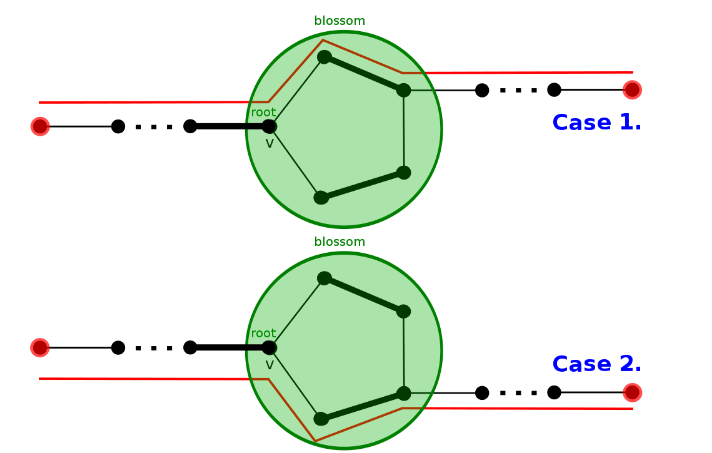将花缩成一个点后，环上所有点变成黑点，并可以在交错树上向外延伸。

具体实现中，不需要真正地记录花，只需要记录每个点对应花根位置 $fa$（本质是个并查集）；同时为了方便上述两种情况的判断，对于所有黑点，记录交错树上从根开始连向当前点的非匹配边 $pre$（对于非花点 $i$，$pre_i$ 就是父节点）。

每当找到黑-黑边（S-S 边）时进行缩花（shrink）操作，花托就是两点的 LCA ，可以暴力求出；将花内所有白点变黑入队，并更新这些点的 $pre$ 。由于实现比较容易，下面不解释地给出参考代码（后来还是写了一些注释便于理解）。

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
int mat[N],color[N],n; // color 1: black 2: white
int pre[N]; // walk through a unmatched edge
int fa[N]; // union-find set
vector<int>G[N];
queue<int>Q; 
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void rev(int p){ // reverse augment path from rt to p
    // !!!!!!!!!!!! graph needs to be [1,n]
    if(p){
        rev(mat[pre[p]]);
        mat[p]=pre[p];mat[pre[p]]=p;
    }
}
void shrink(int u,int v,int r){
    // shrink odd cycle into 1 point: color all along to black ([x])
    // pre: -> [x] ->
    //             <- [y] <-
    while(find(u)!=r){
        // [pre[mat[u]] <- mat[u] -- [u] -- [v]
        // turn into (-> stands for pre)
        //         [u]  <- [v]    -- []  -> []
        pre[u]=v;
        fa[mat[u]]=fa[u]=r;
        if(color[mat[u]]==2)color[mat[u]]=1,Q.push(mat[u]);
        v=mat[u];u=pre[v];
    }
}
int vis[N];
int lca(int x,int y){
    static int t=0;
    ++t;
    while(1){
        if(vis[x=find(x)]==t)return x;
        else if(x)vis[x]=t;
        x=pre[mat[x]];
        swap(x,y);
    }
}
int augment(int rt){
    int i;
    for(i=0;i<=n;i++)fa[i]=i,color[i]=pre[i]=0;
    color[rt]=1;
    Q=queue<int>({rt});
    while(!Q.empty()){
        p=Q.front();Q.pop();
        assert(color[p]==1); // black
        for(auto q:G[p]){
            if(color[q]==1){
                int r=lca(p,q); // root of flower
                shrink(p,q,r);
                shrink(q,p,r);
            }
            else if(!color[q]){
                color[q]=2; // white
                pre[q]=p;
                if(!mat[q]){
                    rev(q);
                    return 1;
                }else{
                    color[mat[q]]=1;
                    Q.push(mat[q]);
                }
            }
        }
    }
    return 0;
}
int maxmatch(){
    int i,m;
    scanf("%d%d",&n,&m);
    int ans=0;
    for(i=0;i<m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        G[x].pb(y);G[y].pb(x);
        if(!mat[x]&&!mat[y])mat[x]=y,mat[y]=x,ans++;
    }
    for(i=1;i<=n;i++)if(!mat[i])ans+=augment(i);
    return ans;
}

二分图最大权匹配

和二分图最大匹配一样，最大权匹配也可以通过网络流那一套求解：将每条边的边权看做一个费用，然后求一下最大费用最大流即可。但为了扩展到一般图，考虑 KM 算法。

学之前，我对二分图最大权匹配的印象仅停留在 KM 算法的板子上，没有真正去理解 KM 算法。下面简单介绍一下 KM 算法（如果你是第一次学习 KM 算法，推荐一个比较有趣的引入：KM算法详解+模板，仅看找对象部分大致了解一下即可）。

最大权完美匹配

我们先考虑最大权完美匹配（最大权匹配可以通过增加零边变成完美匹配）。设对于边 $e$，选/不选该边表示为 $x_e=0$ 或 $x_e=1$；设 $\delta(v)$ 表示 $v$ 所连的边集，则我们要求的最大权匹配即为

$\max\sum_{e\in E} w(e)x_e$，满足条件 $\left\{\begin{aligned}&x(\delta(v))=1:\forall v\in V\\&x_e\in{0, 1}:\forall e\in E\end{aligned}\right.$

这是一个整数规划问题，通过原始对偶（Primal-Dual）思想转化为对偶问题：

$\min \sum_{v\in V}z_v$，满足条件 $\left\{\begin{aligned}&z_e=z_u+z_v-w(e)\ge 0:\forall e\in E\\& z_u\ge 0:\forall v\in V\end{aligned}\right.$

同时，根据互补松弛条件， $x_e>0\Rightarrow z_e=0$。即，对于选中的边 $e$，必有 $z_e=0$。

这里的 $z$ 就是 $KM$ 算法中的顶标（vertex labeling）。定义边 $e(u,v)$ 为”等边“当且仅当 $z_u+z_v=w(e)$，也即 $z_e=0$，根据上述互补松弛条件，匹配只能在等边构成的子图上建。初始时，左部（黑点）每个点的顶标均为其能够连到的最大边权，右部（白点）每个点的顶标均为 $0$。与匈牙利算法类似，每次增广先在“等边”构成的一张二分子图上进行尝试匹配，如果匹配不到，则松弛（将标准放低一些）后继续尝试；直至所有边都成为等边仍未找到增广，算法结束。

松弛的目的是使一些新边成为等边，加入二分子图，让左部点能尝试匹配的点更多；同时保证已有匹配边 $z_e=0$ 。对于所有未匹配边，求出最小的 $delta=\min_e z_e=z_u+z_v-w(e)$，然后将交错树中黑点的顶标降低 $delta$，交错树中白点的顶标增加 $delta$。这样暴力做的复杂度是 $O(n^4)$，下面给出参考代码。

暴力实现

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const ll inf=0x3f3f3f3f3f3f3f3f;
ll w[N][N],lx[N],ly[N];
int mat[N],visx[N],visy[N],n;
int dfs(int x){
    visx[x]=1;
    int y;
    for(y=1;y<=n;y++){
        if(!visy[y]&&lx[x]+ly[y]==w[x][y]){
            visy[y]=1;
            if(!mat[y]||dfs(mat[y]))return mat[y]=x,1;
        }
    }
    return false;
}
ll km(){
    int i,x,y;
    memset(lx,0,sizeof(lx));
    memset(ly,0,sizeof(ly));
    memset(mat,0,sizeof(mat));
    for(x=1;x<=n;x++)
        for(y=1;y<=n;y++)
            lx[x]=max(lx[x],w[x][y]);
    for(i=1;i<=n;i++){
        while(1){
            memset(visx,0,sizeof(visx));
            memset(visy,0,sizeof(visy)); 
            if(dfs(i))break;
            ll d=inf;
            for(x=1;x<=n;x++)
                for(y=1;y<=n;y++)
                    if(visx[x]&&!visy[y])
                        d=min(d,lx[x]+ly[y]-w[x][y]);
            if(d==inf)break;
            for(x=1;x<=n;x++)if(visx[x])lx[x]-=d;
            for(y=1;y<=n;y++)if(visy[y])ly[y]+=d;
        }
    }
    ll ans=0;
    for(i=1;i<=n;i++)ans+=w[mat[i]][i];
    return ans;
}

不太行，考虑优化。

优化方案

一种可行的方案是，对于所有右部点 $y$，记录 $slv_y=\text{argmin}_{x\in T}(z_x+z_y-w(x,y))$ ，即固定了 $y$ 后， $z_e$ 最小值对应 $x$ ，其中 $T$ 为交错树。每次扩展的时候，都是取 $slv_y$ 计算出结果最小的 $y$ 进行扩展，这样就能够保留已有的交错树进而继续增广，每次增广的复杂度变成 $O(n^2)$，总复杂度 $O(n^3)$。下面给出示例代码，其中为方便增广，使用 $pre$ 记录黑点在交错上父亲的父亲（最近黑点祖先）。

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
const ll inf=0x3f3f3f3f3f3f3f3f;
ll w[N][N],lx[N],ly[N];
int mx[N],my[N],visx[N],visy[N],n;
int slv[N],pre[N];
queue<int>Q;
ll calc_slv(int u,int v){return lx[u]+ly[v]-w[u][v];}
void add_to_tree(int x){ // add x to tree, update all slv[y]
    Q.push(x);
    visx[x]=1;
    int y;
    for(y=1;y<=n;y++)
        if(!slv[y]||calc_slv(x,y)<calc_slv(slv[y],y))slv[y]=x;
}
void link(int x,int y){
    int tx,ty;
    while(x){
        tx=pre[x];ty=mx[x];
        my[y]=x;mx[x]=y;
        x=tx,y=ty;
    }
}
int augment(int p){
    int x,y;
    while(1){
        while(!Q.empty()){
            int x=Q.front();Q.pop();
            for(y=1;y<=n;y++)if(!visy[y]&&!calc_slv(x,y)){
                visy[y]=1;
                if(!my[y])return link(x,y),1;
                pre[my[y]]=x;
                add_to_tree(my[y]);
            }
        } 
        ll d=inf;
        for(y=1;y<=n;y++)
            if(!visy[y])
                d=min(d,calc_slv(slv[y],y));
        if(d==inf)break;
        for(x=1;x<=n;x++)if(visx[x])lx[x]-=d;
        for(y=1;y<=n;y++)if(visy[y])ly[y]+=d;
        // add new edges
        for(y=1;y<=n;y++)if(!visy[y]&&!calc_slv(slv[y],y)){
            visy[y]=1;
            if(!my[y])return link(slv[y],y),1;
            pre[my[y]]=slv[y]; // tree: slv -> y == my[y], == stands for match
            add_to_tree(my[y]);
        }
    }
    return 0;
}
ll km(){
    int i,x,y;
    memset(lx,0,sizeof(lx));
    memset(ly,0,sizeof(ly));
    memset(mx,0,sizeof(mx));
    memset(my,0,sizeof(my));
    for(x=1;x<=n;x++)
        for(y=1;y<=n;y++)
            lx[x]=max(lx[x],w[x][y]);
    for(i=1;i<=n;i++){
        memset(visx,0,sizeof(visx));
        memset(visy,0,sizeof(visy)); 
        memset(slv,0,sizeof(slv)); 
        Q=queue<int>();
        add_to_tree(i);
        augment(i);
    }
    ll ans=0;
    for(i=1;i<=n;i++)ans+=w[my[i]][i];
    return ans;
}

Bonus

还有一种使用同样思想，利用局部最优获得全局最优的实现方式。对于每一个黑点 $x$，找到某个白点加入交错树，这个过程中始终是选择 $z_e$ 较小的边进行扩展的，直到找到 $x$ 所对应的增广路。

假设当前已经处理到 $x$，$1\dots x-1$ 都已经有对应的增广路了。设对于未匹配白点 $y$，与所有已匹配黑点 $x$ 中的 $z_e$ 最小值为 $slack_y$，有 $slack_y=\min_{i\in[1,x)}z_i+z_y-w_{i,y}$。那么加入交错树的 $yy=\text{argmin}( slack_y)$；同时，根据 $yy$ 的 $z_{(i,yy)}$ 去更新黑白已匹配点的顶标和下一轮的 $slack$，同时将 $mat_{yy}$ 这个黑点加入交错树（如果 $yy$ 没有匹配那就说明增广路找着了，退出循环）。

这样的方法对于顶标的初始值没有要求（可以不初始化），每次得到的是 $x$ 的局部最优解，但由于可以进行增广，因此最后得到的也是全局最优解，非常巧妙。下面给出代码。其中 $pre$ 记录的是白点在交错树上父亲的父亲（最近白点祖先），$visy$ 记录白点 $i$ 是否在交错树中。这个实现常数略小一点。

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
const ll inf=0x3f3f3f3f3f3f3f3f;
ll a[N],p[N],b[N],c[N];
ll w[N][N],slack[N],lx[N],ly[N];
// for right points
//   pre: last right point in augment path
//   visy: if i is in augment path
//   left: left match
int pre[N],visy[N],left[N]; 
int n;
void augment(int p){
    int i,x=p,y=0,yy;
    memset(pre,0,sizeof(pre));
    memset(slack,0x3f,sizeof(slack));
    left[0]=p;
    while(1){
        x=left[y],visy[y]=1;
        ll delta=inf;
        for(i=1;i<=n;i++){
            if(visy[i])continue;
            ll d=lx[x]+ly[i]-w[x][i];
            if(slack[i]>d)slack[i]=d,pre[i]=y;
            if(slack[i]<delta)delta=slack[i],yy=i;
        }
        for(i=0;i<=n;i++){
            if(visy[i])lx[left[i]]-=delta,ly[i]+=delta;
            else slack[i]-=delta;
        }
        y=yy;
        if(left[y]==-1)break;
    }
    // reverse augment path
    while(y)left[y]=left[pre[y]],y=pre[y]; 
}
ll km(){
    int i,j;
    memset(left,-1,sizeof(left));
    memset(lx,0,sizeof(lx));
    memset(ly,0,sizeof(ly));
    for(i=1;i<=n;i++){
        memset(visy,0,sizeof(visy));
        augment(i);
    }
    ll res=0;
    for(i=1;i<=n;i++)if(left[i]>0)res+=w[left[i]][i];
    return res;
}

其他匹配的形式

上述讨论的都是左右部大小相等的完全二分图上的最大权完美匹配；对于 $n_1\neq n_2$ 的情况，可以补齐不足元素进行计算；对于不要求完美匹配的最大权匹配，可以直接应用本模板；对于非完全二分图，增广过程中对不存在的边进行特判即可。

一般图最大权匹配

仍然考虑 KM 算法在带花树上跑的过程。当进行松弛操作时，如果仍然按照上面的处理方式，白点 $+delta$，黑点 $-delta$，那么对于一个缩成点的花来说，其中有很多交错树上的边 $(u,v)$，$u$ 和 $v$ 的顶标都被加或者减掉了 $delta$，导致这条边不满足 $z_e\ge 0$ 的条件。于是需要对于整个花 $B$，设置额外的花标 $z_B$，在松弛时额外对所有黑花 $+2delta$，对白花 $-2delta$，才能保持平衡。

对偶问题

设 $O$ 为大小为 $\ge 3$ 奇数的集合的集合（包含所有花），$\gamma(S)$ 表示 $S$ 集合中的边，这个过程仍然可通过线性规划转化为对偶问题：

$\max \sum_{e\in E}w(e)x_e$，满足条件 $\left\{\begin{aligned}&x(\delta(v))=1:\forall v\in V\\&x_e\in{0,1}:\forall e\in E\\&x(\gamma(B))\le \lfloor\frac{|B|}{2}\rfloor:\forall B\in O\end{aligned}\right.$

对偶问题

$\min \sum_{v\in V}z_v+\sum_{B\in O}\lfloor\frac{|B|}{2}\rfloor z_B$，满足条件 $\left\{\begin{aligned}&z_B\ge 0:\forall B\in O\\&z_e=z_u+z_v-w(e)+\sum_{B\in O,(u,v)\in \gamma(B)} Z_B \ge 0:\forall e\in E\end{aligned}\right.$

与二分图最大权匹配相同，根据互补松弛条件， $x_e>0\Rightarrow z_e=0$。即，对于选中的边 $e$，必有 $z_e=0$；除此以外，还有 $z_B>0\Rightarrow x(\gamma(B))=\lfloor\frac{|B|}2\rfloor$，即所有 $z_B>0$ 的集合 $B$，都被选了集合大小一半的边，也即 $B$ 是一朵花。同时，我们加入一个条件： $z_B>0\Rightarrow x(\delta(B))=1$，即只有花 $B$ 向外连了一条边的时候， $z_B>0$ 才是有意义的。这很容易根据 $z_B$ 的用途理解。

具体实现

因此，我们需要维护的就是：

  1. 任意边 $z_e\ge 0$，取等时是交错树里（包括形成花的边）的边；
  2. $z_B\ge 0$。

通过类似 KM 的办法，我们就可以容易地维护带花树了！本文完

难点就在它的实现步骤。这里我分享一下通过借鉴一派 UOJ 神仙提交代码，提纯结晶后得到的模板实现思路与细节。min25 的板子真心看不懂，有懂哥欢迎补充！

先摆一下是如何存储这张带花树的：使用 $edge$ 类型存边，大有讲究！对于有花参与的连边，$edge$ 存储的 $u,v$ 不是花本身，而是花内真实节点的边。

1
2
3
4
5
6
7
8
9
10
11
12
13
#define N M*2+1
struct edge{
    int u,v;T w;
    edge(){}
    edge(int u,int v,T w):u(u),v(v),w(w){}
};
// Graph
int n,n_x; // [1, n]: point; [n+1, n_x]: flower
edge g[N][N]; // adjacent matrix
// flower
vector<int>flower[N]; // nodes in flower i (outer flower)
int root[N]; // flower root, root<=n root=i: normal nodes
int flower_from[N][N]; // flower_from[b][x]: outermost flower in b that contains x

其中，与普通带花树不同，这里的花是额外进行存储的（存储在 $n+1$ 到 $n_x$ 内），因此需要开两倍空间。花可以嵌套，而且花需要在某些时刻进行展开（后面会详细讲述），因此需要保存额外的信息。对于一个花 $B$，存储其根 $root$，对于花内任意点有 $root_{i\in B}=B$；存储花内所有节点 $flower_B$，是以花托为起始的环；同时，花内每一点 $i$ 保存“花内最大父花” flower_from[B][i] 表示最大的包含 $i$ 的 $B$ 的子花。

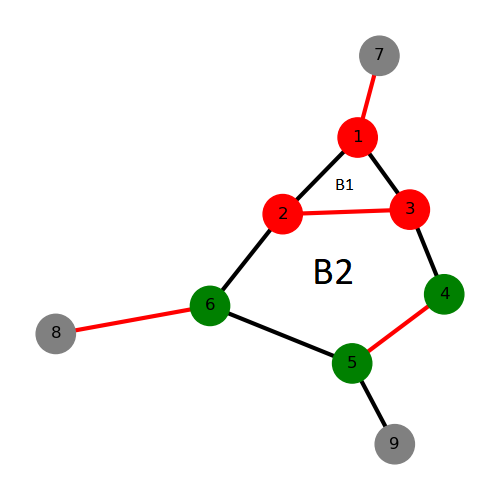对于上面这朵嵌套花：${1,2,3}\in B_1,{B_1,4,5,6}\in B_2$，存储为：

1
2
3
4
5
6
7
8
flower[B1]={1,2,3} // 1 是花托，按照某个顺序转圈，也可能是 {1,3,2}
flower[B2]={6,B1,4,5} // 6 是花托，按照某个顺序转圈，也可能是 {6,5,4,B1}
root[1]=root[6]=root[B1]=root[B2]=B2 // i 最外层的花托
flower_from[B2][B1]=B1
flower_from[B2][1]=B1
flower_from[B2][4]=4
flower_from[B1][1]=1
root[7]=7 // 非花点 root 为自身

然后是 $slack$ 和匹配相关：

1
2
3
4
5
6
7
8
9
10
// slack
T label[N]; // node label, [1, n] point label, [n+1, n_x] flower label
int col[N]; // color saved at flower root
int slv[N]; // slack node of NON LEAF NODES, slv[y]=x z(x,y) min_x
// match
int mat[N]; // match, mat[x]=y (x,y)\in E
int fa[N]; // fa in cross tree
int vis[N]; // if in path

queue<int>Q; // bfs queue

$label$ 也就是对偶问题里的 $z$。$col$ 是节点颜色，为黑色或白色。$slv_y$ 表示与 $y$ 邻接且不在一朵花的、 $z(x,y)$ 最小的 $x$，因为仅会在 $x,y$ 不在一朵花中的时候用到，计算时可以直接 $z_x+z_y-w(x,y)$。 $slv$ 的目的是计算松弛：每次松弛时，找到的边只有两种，即未访问点 $y$ 和某个黑点 $x$ 之间的边；已访问的黑点 $y$ 和某个已访问且不同花黑点之间的边。因此通过 $slv$ 可以方便地进行计算，总复杂度 $O(n^3)$。

$mat$ 可能是花之间的匹配，即 $mat_x=y$ 中 $x>n,y>n$ 均是被允许的。$vis$ 只用来计算 $LCA$ ，可以暂时忽略。$fa$ 表示某白点在交错树上的父节点。注意到黑点交错树上的父节点是 $mat_i$，利用这两个东西就可以在交错树上追溯到根了。

接下来是对 $slv$ 的更新和计算：

1
2
3
4
5
6
7
8
9
10
11
// calculate slv
inline T calc_slv(edge e){return label[e.u]+label[e.v]-e.w;}
inline void update_slv(int u,int v){
    if(!slv[v]||calc_slv(g[u][v])<calc_slv(g[slv[v]][v]))slv[v]=u;
}
inline void recalc_slv(int u){
    slv[u]=0;
    for(int i=1;i<=n;i++)
        if(g[i][u].w>0&&root[i]!=u&&col[root[i]]==1)
            update_slv(i,u);
}

对于 BFS 队列，在将花加入队列时需要将花中所有点都加入队列；设置最外层花时，对于花中所有点都要进行设置。

1
2
3
4
5
6
7
8
9
10
11
// only push nodes, not flowers
void q_push(int x){
    if(x<=n)Q.push(x);
    else for(auto p:flower[x])q_push(p);
}

// set root of all nodes in x to r
void set_root(int x,int r){
    root[x]=r;
    if(x>n)for(auto p:flower[x])set_root(p,r);
}

获取某朵花 $b$ 中，从花托到 $x$ 一条交错路径：对花连出去边的两种情况分别处理，返回一个指针。

1
2
3
4
5
6
7
8
// return a (+-)^k path in flower b from root[b] to x
int get_even_path_in_flower(int b,int x){
    int pr=find(flower[b].begin(),flower[b].end(),x)-flower[b].begin();
    assert(b>n&&b<=n_x&&pr<flower[b].size()); // b is flower, x in b
    if(pr%2==0)return pr;
    reverse(flower[b].begin()+1,flower[b].end());
    return flower[b].size()-pr;
}

某次增广使得需要设置 $u$ 匹配 $v$，$u$ 可能是花（$v$ 不管）：对于 $u$ 为花的情况，从花托到真实 $u$ 的边都进行翻转匹配，最后花托移位，旋转花到正确位置。

1
2
3
4
5
6
7
8
9
10
11
12
// set (u->v) match, can be flower
void set_match(int u,int v){
    mat[u]=g[u][v].v;
    if(u>n){
        edge e=g[u][v];
        int xr=flower_from[u][e.u];
        int pr=get_even_path_in_flower(u,xr);
        for(int i=0;i<pr;i++)set_match(flower[u][i],flower[u][i^1]);
        set_match(xr,v);
        rotate(flower[u].begin(),flower[u].begin()+pr,flower[u].end()); // change receptacle
    }
}

连接两个不在同一个花里的 S 点（黑点）：两个点到根的路径，加上两点之间的边，能构成一条增广路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// link 2 S points
void side_augment(int u,int v){
    int nv=root[mat[u]],nu=root[fa[nv]];
    while(1){
        set_match(u,v);
        u=nu,v=nv;
        if(!nv)break;
        set_match(nv,nu);
        nv=root[mat[u]],nu=root[fa[nv]];
    }
}
void linkSS(int u,int v){
    side_augment(u,v); 
    side_augment(v,u);
}

暴力查询两点 LCA：直接跳父链打标记。

1
2
3
4
5
6
7
8
9
10
11
12
int get_lca(int u,int v){
    static int t=0;
    ++t; // to avoid clearing vis
    while(u||v){
        if(vis[u]==t)return u;
        vis[u]=t;
        u=root[mat[u]];
        if(u)u=root[fa[u]];
        if(!u)swap(u,v);
    }
    return 0;
}

增加一朵奇花：需要申请一个 $id$ 设为 $b$，清空所有数据，并重构。需要重构的部分有：颜色；匹配（继承花托的匹配）；花内节点；花内节点的 root、flower_from；邻接矩阵；slv 值。其中，邻接矩阵取的是 $z_e$ 最小的值，这可以保证正确性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void add_blossom(int u,int v,int r){
    int i,b=n+1;
    while(b<=n_x&&root[b])b++;
    if(b>n_x)++n_x;
    // clear
    col[b]=1;label[b]=0;mat[b]=mat[r];flower[b].clear();
    for(i=1;i<=n_x;i++)g[i][b].w=g[b][i].w=0;
    for(i=1;i<=n;i++)flower_from[b][i]=0;
    // construct flower
    while(u!=r){
        flower[b].pb(u);u=root[mat[u]];q_push(u);
        flower[b].pb(u);u=root[fa[u]];
    }
    flower[b].pb(r);
    reverse(flower[b].begin(),flower[b].end());
    while(v!=r){
        flower[b].pb(v);v=root[mat[v]];q_push(v);
        flower[b].pb(v);v=root[fa[v]];
    }
    // set as outermost flower
    set_root(b,b);
    // calculate slack
    for(auto p:flower[b]){
        for(i=1;i<=n_x;i++){
            // set to min slave
            if(!g[b][i].w||calc_slv(g[p][i])<calc_slv(g[b][i])){
                g[b][i]=g[p][i];
                g[i][b]=g[i][p];
            }
        }
        for(i=1;i<=n;i++)if(flower_from[p][i])flower_from[b][i]=p;
    }
    recalc_slv(b);
}

尝试增广一条等边：如果对点未染过色，则必然已经有匹配，将其匹配染色后丢入队列；如果对点是黑点，分两种情况，如果 $LCA=0$ 即不在同一花内，则 linkSS，否则添加花。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// found_edge
int augment_path(edge e){
    int u=root[e.u],v=root[e.v];
    if(!col[v]){
        assert(mat[v]);
        fa[v]=e.u;
        col[v]=2;
        int nu=root[mat[v]];
        slv[nu]=slv[v]=0;
        col[nu]=1;
        q_push(nu);
    }else if(col[v]==1){
        int r=get_lca(u,v);
        if(r)add_blossom(u,v,r);
        else return linkSS(u,v),1;
    }
    return 0;
}

一次增广：将所有未匹配点入队进行 BFS。先尝试使用当前 $label$ 下的等边构成的子图跑增广，如果增广成功直接返回。如果无法成功，则需要计算出松弛的大小，并将 $z_u,z_B$ 分别进行更新。更新后，如果某点 $(i,slv_i)$ 路径被加入等边子图中，则进行尝试增广。如果没有，则进行新的一轮增广。

有几个细节需要注意：

  1. 白花 $z_B$ 会减掉一个正数，但要求保证 $z_B\ge 0$。
  2. 如何计算松弛的大小

由于有 $z_B\ge 0$ 这样的特殊约束，当一朵白花 $z_B=0$ 时，需要对其进行开花操作 expand_blossom，即将花展开，将花中在交错树上的部分链加入交错树中，并将其他节点设置为“没有听说过”，即 $col_i=0$。

上面也提到过，每次松弛需要考虑的只有下列情况：

  1. 某个黑点 $u$ 和某个未匹配点 $v$ 之间的边
  2. 某两个不在同一个花内的黑点 $u,v$ 之间的连边

加上 $z_B\ge 0,z_u\ge 0$ 两个条件，总共需要找的是四种情况，其中要用到 $\frac{z_B}2$、$\frac{z_e}{2}$ 的形式，因此边权整体乘二；但 $z_B$ 要小于零了可以拆花，$z_u$ 要小于零可就真的找不到匹配路径了，因此如果某次结束后 $z_u=0$，直接返回增广失败。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
int augment(){
    int i;
    memset(col,0,sizeof(int)*(n_x+1));
    memset(slv,0,sizeof(int)*(n_x+1));
    memset(fa,0,sizeof(int)*(n_x+1));
    Q=queue<int>();
    for(i=1;i<=n_x;i++)
        if(root[i]==i&&!mat[i]){
            // add all unmatched points
            col[i]=1;
            q_push(i);
        }
    if(Q.empty())return 0;
    while(1){
        while(!Q.empty()){
            int p=Q.front();Q.pop();
            assert(col[root[p]]==1);
            for(i=1;i<=n;i++){
                if(g[p][i].w==0||root[i]==root[p])continue;
                // not in same flower
                T d=calc_slv(g[p][i]);
                if(!d){if(augment_path(g[p][i]))return 1;}
                else if(col[root[i]]!=2)update_slv(p,root[i]);
            }
        }
        T delta=INF;
        // calc delta
        for(i=1;i<=n;i++)if(col[root[i]]==1)delta=min(delta,label[i]);
        for(i=n+1;i<=n_x;i++)if(root[i]==i&&col[i]==2)delta=min(delta,label[i]/2);
        for(i=1;i<=n_x;i++){
            if(root[i]!=i||!slv[i])continue;
            if(!col[i])delta=min(delta,calc_slv(g[slv[i]][i]));
            else if(col[i]==1)delta=min(delta,calc_slv(g[slv[i]][i])/2);
        }
        // update label
        for(i=1;i<=n;i++){
            if(col[root[i]]==1)label[i]-=delta;
            else if(col[root[i]]==2)label[i]+=delta;
        }
        for(i=n+1;i<=n_x;i++){
            if(root[i]!=i)continue;
            if(col[i]==1)label[i]+=2*delta;
            else if(col[i]==2)label[i]-=2*delta;
        }
        for(i=1;i<=n;i++)if(label[i]<=0)return 0;
        for(i=1;i<=n_x;i++){
            if(root[i]!=i||!slv[i]||root[slv[i]]==i)continue;
            if(calc_slv(g[slv[i]][i])==0&&augment_path(g[slv[i]][i]))return 1;
        }
        // expand
        for(i=n+1;i<=n_x;i++)
            if(root[i]==i&&col[i]==2&&label[i]==0)
                expand_blossom(i);
    }
    return 0;
}

两开花的具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// only expand outermost blossom b, b is T(white) blossom
void expand_blossom(int b){
    int i,x;
    for(auto p:flower[b])set_root(p,p);
    x=flower_from[b][g[b][fa[b]].u];
    // [0,pr]: (+-)^k, insert into tree, add black to queue
    int pr=get_even_path_in_flower(b,x);
    col[x]=2;fa[x]=fa[b];
    for(i=0;i<pr;i+=2){
        // from bottom to upper layer in tree
        int white=flower[b][i];
        int black=flower[b][i+1];
        col[black]=1;col[white]=2;
        fa[white]=g[black][white].u;
        slv[black]=slv[white]=0;
        q_push(black);
    }
    // others: color=0
    for(i=pr+1;i<flower[b].size();i++){
        col[flower[b][i]]=0;
        recalc_slv(flower[b][i]);
    }
    // delete b
    root[b]=0;
    flower[b].clear();
}

参考代码

加上主函数，下面放一下完整的模板实现（题目是 UOJ #81）：

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
#define M 403
using T=ll;
const T INF=0x3f3f3f3f3f3f3f3f;
namespace blossom_tree{
#define N M*2+1
    struct edge{
        int u,v;T w;
        edge(){}
        edge(int u,int v,T w):u(u),v(v),w(w){}
    };
    // Graph
    int n,n_x; // [1, n]: point; [n+1, n_x]: flower
    edge g[N][N]; // adjacent matrix
    // flower
    vector<int>flower[N]; // nodes in flower i (outer flower)
    int root[N]; // flower root, root<=n root=i: normal nodes
    int flower_from[N][N]; // flower_from[b][x]: outermost flower in b that contains x
    // slack
    T label[N]; // node label, [1, n] point label, [n+1, n_x] flower label
    int col[N]; // color saved at flower root
    int slv[N]; // slack node of NON LEAF NODES, slv[y]=x z(x,y) min_x
    // match
    int mat[N]; // match, mat[x]=y (x,y)\in E
    int fa[N]; // fa in cross tree
    int vis[N]; // if in path
    
    queue<int>Q; // bfs queue
    
    // calculate slv
    inline T calc_slv(edge e){return label[e.u]+label[e.v]-e.w;}
    inline void update_slv(int u,int v){if(!slv[v]||calc_slv(g[u][v])<calc_slv(g[slv[v]][v]))slv[v]=u;}
    inline void recalc_slv(int u){
        slv[u]=0;
        for(int i=1;i<=n;i++)if(g[i][u].w>0&&root[i]!=u&&col[root[i]]==1)update_slv(i,u);
    }
    
    // only push nodes, not flowers
    void q_push(int x){
        if(x<=n)Q.push(x);
        else for(auto p:flower[x])q_push(p);
    }
    
    // set root of all nodes in x to r
    void set_root(int x,int r){
        root[x]=r;
        if(x>n)for(auto p:flower[x])set_root(p,r);
    }
    
    // return a (+-)^k path in flower b from root[b] to x
    int get_even_path_in_flower(int b,int x){
        int pr=find(flower[b].begin(),flower[b].end(),x)-flower[b].begin();
        assert(b>n&&b<=n_x&&pr<flower[b].size()); // b is flower, x in b
        if(pr%2==0)return pr;
        reverse(flower[b].begin()+1,flower[b].end());
        return flower[b].size()-pr;
    }
    
    // set (u,v) match, can be flower
    void set_match(int u,int v){
        mat[u]=g[u][v].v;
        if(u>n){
            edge e=g[u][v];
            int xr=flower_from[u][e.u];
            int pr=get_even_path_in_flower(u,xr);
            for(int i=0;i<pr;i++)set_match(flower[u][i],flower[u][i^1]);
            set_match(xr,v);
            rotate(flower[u].begin(),flower[u].begin()+pr,flower[u].end()); // change receptacle
        }
    }
    
    // link 2 S points
    void side_augment(int u,int v){
        int nv=root[mat[u]],nu=root[fa[nv]];
        while(1){
            set_match(u,v);
            u=nu,v=nv;
            if(!nv)break;
            set_match(nv,nu);
            nv=root[mat[u]],nu=root[fa[nv]];
        }
    }
    void linkSS(int u,int v){
        side_augment(u,v); 
        side_augment(v,u);
    }
    
    int get_lca(int u,int v){
        static int t=0;
        ++t; // to avoid clearing vis
        while(u||v){
            if(vis[u]==t)return u;
            vis[u]=t;
            u=root[mat[u]];
            if(u)u=root[fa[u]];
            if(!u)swap(u,v);
        }
        return 0;
    }
    
    void add_blossom(int u,int v,int r){
        int i,b=n+1;
        while(b<=n_x&&root[b])b++;
        if(b>n_x)++n_x;
        // clear
        col[b]=1;label[b]=0;mat[b]=mat[r];flower[b].clear();
        for(i=1;i<=n_x;i++)g[i][b].w=g[b][i].w=0;
        for(i=1;i<=n;i++)flower_from[b][i]=0;
        // construct flower
        while(u!=r){
            flower[b].pb(u);u=root[mat[u]];q_push(u);
            flower[b].pb(u);u=root[fa[u]];
        }
        flower[b].pb(r);
        reverse(flower[b].begin(),flower[b].end());
        while(v!=r){
            flower[b].pb(v);v=root[mat[v]];q_push(v);
            flower[b].pb(v);v=root[fa[v]];
        }
        // set as outermost flower
        set_root(b,b);
        // calculate slack
        for(auto p:flower[b]){
            for(i=1;i<=n_x;i++){
                // set to min slave
                if(!g[b][i].w||calc_slv(g[p][i])<calc_slv(g[b][i])){
                    g[b][i]=g[p][i];
                    g[i][b]=g[i][p];
                }
            }
            for(i=1;i<=n;i++)if(flower_from[p][i])flower_from[b][i]=p;
        }
        recalc_slv(b);
    }
    
    // only expand outermost blossom b, b is T(white) blossom
    void expand_blossom(int b){
        int i,x;
        for(auto p:flower[b])set_root(p,p);
        x=flower_from[b][g[b][fa[b]].u];
        // [0,pr]: (+-)^k, insert into tree, add black to queue
        int pr=get_even_path_in_flower(b,x);
        col[x]=2;fa[x]=fa[b];
        for(i=0;i<pr;i+=2){
            // from bottom to upper layer in tree
            int white=flower[b][i];
            int black=flower[b][i+1];
            col[black]=1;col[white]=2;
            fa[white]=g[black][white].u;
            slv[black]=slv[white]=0;
            q_push(black);
        }
        // others: color=0
        for(i=pr+1;i<flower[b].size();i++){
            col[flower[b][i]]=0;
            recalc_slv(flower[b][i]);
        }
        // delete b
        root[b]=0;
        flower[b].clear();
    }
    
    // found_edge
    int augment_path(edge e){
        int u=root[e.u],v=root[e.v];
        if(!col[v]){
            assert(mat[v]);
            fa[v]=e.u;
            col[v]=2;
            int nu=root[mat[v]];
            slv[nu]=slv[v]=0;
            col[nu]=1;
            q_push(nu);
        }else if(col[v]==1){
            int r=get_lca(u,v);
            if(r)add_blossom(u,v,r);
            else return linkSS(u,v),1;
        }
        return 0;
    }
    
    int augment(){
        int i;
        memset(col,0,sizeof(int)*(n_x+1));
        memset(slv,0,sizeof(int)*(n_x+1));
        memset(fa,0,sizeof(int)*(n_x+1));
        Q=queue<int>();
        for(i=1;i<=n_x;i++)
            if(root[i]==i&&!mat[i]){
                // add all unmatched points
                col[i]=1;
                q_push(i);
            }
        if(Q.empty())return 0;
        while(1){
            while(!Q.empty()){
                int p=Q.front();Q.pop();
                assert(col[root[p]]==1);
                for(i=1;i<=n;i++){
                    if(g[p][i].w==0||root[i]==root[p])continue;
                    // not in same flower
                    T d=calc_slv(g[p][i]);
                    if(!d){if(augment_path(g[p][i]))return 1;}
                    else if(col[root[i]]!=2)update_slv(p,root[i]);
                }
            }
            T delta=INF;
            // calc delta
            for(i=1;i<=n;i++)if(col[root[i]]==1)delta=min(delta,label[i]);
            for(i=n+1;i<=n_x;i++)if(root[i]==i&&col[i]==2)delta=min(delta,label[i]/2);
            for(i=1;i<=n_x;i++){
                if(root[i]!=i||!slv[i])continue;
                if(!col[i])delta=min(delta,calc_slv(g[slv[i]][i]));
                else if(col[i]==1)delta=min(delta,calc_slv(g[slv[i]][i])/2);
            }
            // update label
            for(i=1;i<=n;i++){
                if(col[root[i]]==1)label[i]-=delta;
                else if(col[root[i]]==2)label[i]+=delta;
            }
            for(i=n+1;i<=n_x;i++){
                if(root[i]!=i)continue;
                if(col[i]==1)label[i]+=2*delta;
                else if(col[i]==2)label[i]-=2*delta;
            }
            for(i=1;i<=n;i++)if(label[i]<=0)return 0;
            for(i=1;i<=n_x;i++){
                if(root[i]!=i||!slv[i]||root[slv[i]]==i)continue;
                if(calc_slv(g[slv[i]][i])==0&&augment_path(g[slv[i]][i]))return 1;
            }
            // expand
            for(i=n+1;i<=n_x;i++)
                if(root[i]==i&&col[i]==2&&label[i]==0)
                    expand_blossom(i);
        }
        return 0;
    }
    
    void init(int _n,vector<pair<T,pii>>edges){
        int i,j;
        n=n_x=_n;
        memset(mat,0,sizeof(mat));
        for(i=0;i<=n;i++){
            root[i]=i;
            flower[i].clear();
            for(j=0;j<=n;j++){
                flower_from[i][j]=(i==j)?i:0;
                g[i][j]=edge(i,j,0);
            }
        }
        T w_max=0;
        for(auto pr:edges){
            int u=pr.se.fi,v=pr.se.se;
            T w=pr.fi;
            g[u][v]=edge(u,v,w*2);
            g[v][u]=edge(v,u,w*2);
            w_max=max(w_max,w);
        }
        for(i=1;i<=n;i++)label[i]=w_max;
    }
    
    pair<int,T>calc(){
        int i,cnt=0;T s=0;
        while(augment())++cnt;
        for(i=1;i<=n;i++)if(mat[i]>i)s+=g[i][mat[i]].w/2;
        return mp(cnt,s);
    }
}
int main(){
    int i,n,m;
    vector<pair<T,pii>>edges;
    scanf("%d%d",&n,&m);
    for(i=0;i<m;i++){
        int u,v;T w;
        scanf("%d%d%lld",&u,&v,&w);
        edges.pb(mp(w,mp(u,v)));
    }
    blossom_tree::init(n,edges);
    printf("%lld\n",blossom_tree::calc().se);
    for(i=1;i<=n;i++)printf("%d ",blossom_tree::mat[i]);
    return 0;
}

参考资料与工具

  1. OI-wiki，一般图最大匹配
  2. Fuyuki，题解 P6113 【模板】一般图最大匹配
  3. 胡拉哥，算法设计技巧：Primal-Dual
  4. wenruo，KM算法详解+模板
  5. Shawn-Yang，KM算法–学习笔记
  6. 陈胤伯，2015 年国家集训队论文《浅谈图的匹配算法及其应用》
  7. jacky860226，general-graph-weighted-match-slides
  8. vfleaking，妈妈我终于会一般图最大权匹配了！
  9. Joris_VR，Maximum Weighted Matching
  10. zhongzihao，一般图最大权（最大）匹配
  11. Kurt Mehlhorn et al.，Implementation of O(nmlogn) weighted matchings in general graphs: the power of data structures
  12. Visualizations of Graph Algorithms
  13. Graph Editor
  14. NetworkX

提交通道

  1. 洛谷
  2. UOJ
  3. Library checker

结语

欢迎纠错与讨论。感谢阅读！