| Solved | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 9/10 | O | O | O | Ø | O | O | O | O | O | . |
- O for passing during the contest
- Ø for passing after the contest
- ! for attempted but failed
- · for having not attempted yet
A
题目描述
有$n$个独立随机变量$x_1,x_2,…,x_n$,第$i$个变量的值$x_i$是从$[l_i,r_i]$中随机选取的整数。
求一个排列$p$,使得$x_{p_1},x_{p_2},…,x_{p_n}$序列的逆序对个数期望尽量少,求这个最小值。
解题思路
一个比较显然的结论是,排列$p$是对区间$[l_i,r_i]$按中点坐标从小到大排序得到的,这样任意两个位置产生逆序对的概率都$\leq \frac12$。
求出排列后,问题转化为求两个长度分别为$len_1,len_2$的区间$[l_1,r_1],[l_2,r_2]$的逆序对期望。画图理解:当$r_1>r_2$时,$x_1\in(r_1,r_2]$区域时,必然贡献一个逆序对,故贡献$\frac {r_2-r_1}{len_1}$;当$l_1>l_2$时,$x_2\in[l_2,l_1)$区域时,必然贡献一个逆序对,故贡献$\frac {l_1-l_2}{len_2}$;当长度为$len$的区间$[l,r]$为两区间的交叉区间时,这个区间的贡献为$\frac 1{len_1len_2}\sum_{i=l}^{r}\sum_{j=i+1}^r1$ $=\frac 1{len_1len_2}\frac{len(len-1)}2$。加起来即可。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
typedef long long ll;
using namespace std;
const int mod=998244353;
int qp(int a,int p){
int ans=1;
for(;p;p>>=1,a=1LL*a*a%mod)if(p&1)ans=1LL*ans*a%mod;
return ans;
}
int inv(ll x){return qp(x,mod-2);}
struct P{
int l,r;
bool operator<(const P&p)const{
return l+r<p.l+p.r;
}
}a[5010];
int L[5010];
int main(){
int i,j,n,l,r;
ll ans=0;
scanf("%d",&n);
for(i=0;i<n;i++)scanf("%d%d",&a[i].l,&a[i].r);
sort(a,a+n);
for(i=0;i<n;i++){
int l1=a[i].l,r1=a[i].r,len1=r1-l1+1;
L[i]=inv(len1);
}
for(i=0;i<n;i++){
for(j=i+1;j<n;j++){
int l1=a[i].l,r1=a[i].r;
int l2=a[j].l,r2=a[j].r;
ll now=0;
if(r1>r2)now+=1LL*(r1-r2)*L[i]%mod;
if(l1>l2)now+=1LL*(l1-l2)*L[j]%mod;
int cl=max(l1,l2),cr=min(r1,r2),len=cr-cl+1;
if(cl<cr)now+=1LL*(len-1)*len/2%mod*L[i]%mod*L[j]%mod;
(ans+=now%mod)%=mod;
}
}
printf("%lld\n",ans);
return 0;
}
B
题目描述
大概是给定一个加密方式,给定加密后的字符串,求加密前的字符串。
解题思路
solved by nikkukun
AC代码 - by nikkukun
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int Idx(char c){
if(islower(c)) return c - 'a';
else return c - 'A' + 26;
}
char Char(int c){
if(c < 26) return 'a' + c;
else return 'A' + c - 26;
}
void Encrypt(string &enc, string key){
int len = key.size();
for(int i=0; i<enc.size(); i++)
enc[i] = Char((Idx(enc[i]) - Idx(key[i % len]) + 52) % 52);
}
const int N = 1000 + 5;
string s[N];
int x[N], y[N];
int main(){
ios::sync_with_stdio(0);
int n, m; cin >> n >> m;
for(int i=1; i<=m; i++)
cin >> x[i] >> y[i];
for(int i=1; i<=n; i++)
cin >> s[i];
for(int i=m; i>=1; i--)
Encrypt(s[y[i]], s[x[i]]);
for(int i=1; i<=n; i++)
cout << s[i] << endl;
return 0;
}
C
题目描述
定义$g(n,k)$为所有包含$n$个点的简单$k$可染色图的边数最大值。$k$可染色的意思是。
给$n,l,r$,求$\sum_{i=l}^rg(n,i)$。($\text {mod 998244353}$)
解题思路
solved by nikkukun
可以猜到,当颜色尽量均分的时候连边数最多。设有$x$种颜色染了$\lfloor\frac nk\rfloor$个点,$y$个点染了$\lfloor\frac nk\rfloor+1$个点。
显然,有$\left [\begin{aligned}&x+y=k\\ &y=n\text{ mod k}=n-k\lfloor\frac nk\rfloor\end{aligned}\right. $。
为了简便,下设$b=\lfloor\frac nk\rfloor$。
连边:完全图边数-同色内不能连边
$=\frac{n(n-1)}2-\frac {b(b-1)}2x-\frac{b(b+1)}2y$
$=\frac 12(n^2-n-2nb)+\frac 12k(b^2+b)$
枚举$k$,故$b$的形式可以用数论分块解决。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
typedef long long ll;
using namespace std;
const int mod=998244353;
ll qp(ll a,ll p){
ll ans=1;
for(;p;p>>=1,a=a*a%mod)if(p&1)ans=ans*a%mod;
return ans;
}
int main(){
int i,j;
ll n,l,r,ans;
ll inv2=qp(2,mod-2);
int t;
scanf("%d",&t);
while(t--){
ans=0;
scanf("%lld%lld%lld",&n,&l,&r);
for(i=l;i<=r;i=j+1){
j=min(r,n/(n/i));
ll b=n/i;
(ans+=(n*n-n-2*n*b)%mod*(j-i+1)%mod*inv2)%=mod;
(ans+=(b*b+b)%mod*(i+j)%mod*(j-i+1)%mod*inv2%mod*inv2)%=mod;
}
printf("%lld\n",(ans+mod)%mod);
}
return 0;
}
D
题目描述
定义$T(G)$表示$G$所有不同生成树形成的集合,$s(G,T)$为同时出现在树$T$和图$G$中的边的数量。
给出两张$n$个点的无向图$G_1,G_2$,求$\sum_{T\in T(G_1)}s(G_2,T)$。
解题思路
之前矩阵树定理没学透,看题解还是不会,遂恶补了一番。
感觉这篇博客写的很好,除了其中一个重要定理的证明以外,其他的都给出了详细的说明和推演。
这个博客概括为以下六条:
- 考虑图$G$的关联矩阵$M_{m\times n}$,设$e$为连接$i,j$的边($i>j$),则$M_{ev}=\left[\begin{aligned}&1&v=i\\ &\text-1&v=j\\ &0&o.w.\end{aligned}\right.$,则基尔霍夫矩阵$L=M^TM$,容易推出$L=D-A$。
- $L$的任意代数余子式值都相等。(非常重要的性质)
- $L$的任意一行、一列的和均为$0$。(非常重要的性质)
- $L$有一个特征值$0$,且特征值$\lambda_i$均$\geq 0$,即$L$是奇异的、半正定的。
- $\det(A_{1,1})=\sum_{S}\det(M_{1,S})^2$,其中$S\in\left(\begin{aligned}\ [m]\\ n-1\end{aligned}\right)$,即$S$为从边集中任意选出的$n-1$个边的集合;$M_1$表示$M$去掉第一列($v=1$)后的矩阵,$M_{1,S}$为$M_1$的行下标位于$S$中(边$e\in e_S$)的子矩阵。
- 当边不连通,有$\det(M_{1,S})=0$;连通时有$\det(M_{1,S})=\pm1$。
因此普通的基尔霍夫矩阵的任意代数余子式为生成树的个数。
以下为个人yy:(不知正误)
在此基础上,我们将$M$稍作修改:
$M’_{ev}=\left[\begin{aligned}&\sqrt{w_e}&v=i\\ &\text-\sqrt{w_e}&v=j\\ &0&o.w.\end{aligned}\right.$
$M’^TM’$得到的矩阵$L’$仍满足上述$2,3,4$性质。此时,$L_{ij}=\left[\begin{aligned}&\sum_{e}w_e[e与i关联]&i=j\\ &\text-w_{ij}&i\neq j\end{aligned}\right.$。
同样有
$\det(A’_{1,1})$
$=\sum_{S}\det(M’_{1,S})^2$。
当边不连通时,有$\det(M’_{1,S})=0$;
连通时有$\det(M’_{1,S})=\pm\sqrt{\Pi_ew_e[e\in S]}$.
同样可以得出,$L’$任意代数余子式为生成树中所有边权之积的和。这就是变元矩阵树定理。
利用变元矩阵树定理可以求解本题:
构造矩阵$L’$,其中设只出现在$G_1$中的边对应的“边权”为$1$,同时出现在$G_1,G_2$中的边对应的“边权”为$x$,那么$L’$的代数余子式$|A(x)|$为一个$x$的$n-1$次多项式,记为$f(x)$,有$f(x)=\sum a_ix^i$,其中$a_i$表示有$i$条公共边的生成树个数。
我们要求的就是$\sum a_i\times i=f’(1)$,
故$ans=f’(1)$
$=|A(1)|\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}A(1)^{-1}[i][j]A’(1)[j][i]$。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
typedef long long ll;
using namespace std;
const int N=440;
const ll mod=998244353;
ll a[N][N],b[N][N],inv[N][N];
int equ,var;
ll qp(ll a,ll p){
ll ans=1;
for(;p;p>>=1,a=a*a%mod)if(p&1)ans=ans*a%mod;
return ans;
}
int Gauss(){
int i,j,k,col,max_r;
ll ans=1;
for(k=0,col=0;k<equ&&col<var;k++,col++){
max_r=k;
for(i=k+1;i<equ;i++)
if(abs(a[i][col])>abs(a[max_r][col]))
max_r=i;
if(!a[max_r][col])return 0;
if(k!=max_r){
for(j=col;j<var;j++)swap(a[k][j],a[max_r][j]);
for(j=0;j<var;j++)swap(inv[k][j],inv[max_r][j]);
ans=mod-ans;
}
ans=ans*a[k][k]%mod;
ll fm=qp(a[k][col],mod-2);
for(j=0;j<var;j++)inv[k][j]=inv[k][j]*fm%mod;
for(j=col+1;j<var;j++)a[k][j]=a[k][j]*fm%mod;
a[k][col]=1;
for(i=0;i<equ;i++)
if(i!=k){
for(j=0;j<var;j++)(inv[i][j]-=inv[k][j]*a[i][col])%=mod;
for(j=col+1;j<var;j++)(a[i][j]-=a[k][j]*a[i][col])%=mod;
a[i][col]=0;
}
}
//消成E|A-1
for(i=var-1;i>=0;i--)
for(j=i-1;j>=0;j--)
for(k=0;k<var;k++)
(inv[j][k]-=a[j][i]*inv[i][k])%=mod;
return ans;
}
char s[N];
int main(){
int i,n,j;
scanf("%d",&n);
equ=var=n-1;
for(i=0;i<n;i++){
scanf("%s",s);
for(j=0;j<n;j++)a[i][j]=(s[j]=='1');
}
for(i=0;i<n;i++){
scanf("%s",s);
for(j=0;j<n;j++)b[i][j]=(s[j]=='1'&&a[i][j]);
}
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(i==j)continue;
a[i][i]+=a[i][j];b[i][i]+=b[i][j];
a[i][j]=-a[i][j];b[i][j]=-b[i][j];
}
}
for(i=0;i<n-1;i++)inv[i][i]=1;
ll ans=Gauss(),ans2=0;
for(i=0;i<var;i++)for(j=0;j<var;j++)
(ans2=ans2+b[i][j]*inv[j][i])%=mod;
printf("%lld",((ans*ans2%mod)+mod)%mod);
return 0;
}
E
题目描述
从$u$到$v$的路径可以分解为沿着向根的方向和离开根的方向两部分,设长度(经过的边数)分别为$l_1,l_2$,则该路径的权值定义为$l_1l_2$。
给定一棵树和$m$条路径,对于每一个$r\in [1,n]$,计算当$r$为根节点时,所有路径的权值和是多少。
解题思路
考虑先计算出$1$为根时的答案,然后换根。
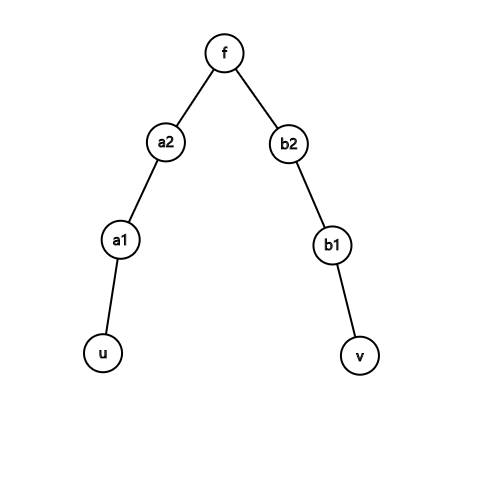
考虑$u,v$路径对各个节点的贡献:设$f=LCA(u,v)$,$l_1=len(u,f),l_2=len(v,f)$,则对$LCA$贡献$l_1l_2$,对$a_2$贡献$(l_1-1)(l_2+1)=l_1l_2-l_2+l_1-1$,对$a_1$贡献$l_1l_2-2l_2+2l_1-4$,……
考虑路径上贡献的差值。
如图,$a_2,f$之间的差值为 $d_1=(l_1-l_2-1)$,$a_1,a_2$之间的差值为$d_2=(l_1-l_2-3)$,这是一个等差数列,在树上胡乱维护一下即可。
具体的维护方式:
差值从下到上构成一个公差为$2$的等差数列,通过树上差分(先维护孩子$\to$父亲的差值之差,再求出每个节点的差值)可以求出这个差值;通过这个差值再从上到下更新每个节点对应的答案。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
typedef long long ll;
using namespace std;
int hd[N],cnt;
struct Edge{
int e,n;
}e[N<<1];
void add(int a,int b){
e[++cnt].e=b;e[cnt].n=hd[a];hd[a]=cnt;
}
int d[N],fa[22][N],lg[N];
void dfs(int now,int f){
d[now]=d[f]+1;
fa[0][now]=f;
int i;
for(i=1;(1<<i)<=d[now];i++)
fa[i][now]=fa[i-1][fa[i-1][now]];
for(i=hd[now];i;i=e[i].n){
int p=e[i].e;
if(p!=f)dfs(p,now);
}
}
int lca(int x,int y){
int i;
if(d[x]<d[y]){int t=x;x=y;y=t;}
while(d[x]>d[y])
x=fa[lg[d[x]-d[y]]][x];
if(x==y)return x;
for(i=lg[d[x]];~i;i--)
if(fa[i][x]!=fa[i][y])
x=fa[i][x],y=fa[i][y];
return fa[0][x];
}
ll f[N],a[N],dt[N];
void dfs2(int p){
int i;
for(i=hd[p];i;i=e[i].n){
int q=e[i].e;
if(q==fa[0][p])continue;
dfs2(q);
a[p]+=a[q]-dt[q];
dt[p]+=dt[q];
}
}
void dfs3(int p){
int i;
for(i=hd[p];i;i=e[i].n){
int q=e[i].e;
if(q==fa[0][p])continue;
f[q]=f[p]+a[q];
dfs3(q);
}
}
int main(){
int i,n,m,u,v;
scanf("%d%d",&n,&m);
for(i=1;i<n;i++){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(i=2;i<=n;i++)lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);
dfs(1,0);
for(i=0;i<m;i++){
scanf("%d%d",&u,&v);
int ff=lca(u,v);
int l1=d[u]-d[ff];
int l2=d[v]-d[ff];
f[1]+=1LL*l1*l2;
a[u]+=l1-l2-(2*l1-1);
a[v]+=l2-l1-(2*l2-1);
a[ff]-=2;
dt[u]-=2;
dt[v]-=2;
dt[ff]+=4;
}
dfs2(1);
dfs3(1);
for(i=1;i<=n;i++)printf("%lld\n",f[i]);
return 0;
}
F
题目描述
给定长度分别为$n,m$的数组$A,B$,矩阵$C=A_i\times B_j$,求$C$中第$k$大的数。
解题思路
solved by qxforever
二分答案,分正负零讨论,分别单调地扫一遍进行处理。
AC代码 - by qxforever
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
typedef long long ll;
const int maxn = 1e5+23;
ll a[maxn],b[maxn],c[maxn],d[maxn];
ll A,B,C,D;
ll n,m,k;
bool check(ll x)
{
ll cnt=0;
if(x>=0) cnt+=n*(m-C-D)+m*(n-A-B)-(m-C-D)*(n-A-B);
for(int i=1,j=C;i<=A;i++){
while(a[i]*c[j]>x&&j>=1) j--;
cnt+=j;
}
for(int i=A,j=D;i;i--){
while(a[i]*d[j]>x&&j>=1) j--;
cnt+=j;
}
for(int i=1,j=1;i<=B;i++){
while(b[i]*c[j]>x&&j<=C) j++;
cnt+=C-j+1;
}
for(int i=B,j=1;i;i--){
while(b[i]*d[j]>x&&j<=D) j++;
cnt+=D-j+1;
}
//printf("%lld\n",cnt);
return cnt<k;
}
int main()
{
cin>>n>>m>>k;k=n*m+1-k;
for(int i=1,j;i<=n;i++){
scanf("%d",&j);
j>0?a[++A]=j:b[++B]=j;
}
for(int i=1,j;i<=m;i++){
scanf("%d",&j);
j>0?c[++C]=j:d[++D]=j;
}
sort(a+1,a+A+1);
sort(b+1,b+B+1);
sort(c+1,c+C+1);
sort(d+1,d+D+1);
ll L=-2e12-1,R=2e12+1;
//check(18);
while(R-L>1){
ll mid=(L+R)/2;
//printf("mid: %lld\n",mid);
if(check(mid)) L=mid;
else R=mid;
}
printf("%lld\n",R);
}
G
题目描述
给定$n$个圆,求它们凸包的周长。
解题思路
先求出来所有公切点的凸包,然后如果相邻两个点在同一个圆上,那么用圆弧连接这两个点,否则用直线连接。
AC代码 - by qxforever
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
using namespace std;
const double pi = acos(-1.0);
const double eps = 1e-10;
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y) {}
bool operator < (const Point &b)
{
return x<b.x||(x==b.x&&y<b.y);
}
};
typedef Point Vector;
Point operator + (Point A,Point B){return Point(A.x+B.x,A.y+B.y);}
Point operator - (Point A,Point B) {return Point(A.x-B.x,A.y-B.y);}
int dcmp(double x)
{
if(fabs(x)<eps) return 0;
return x<0 ? -1 : 1;
}
bool operator == (const Point &a,const Point &b)
{
return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double dot(Vector a,Vector b)
{
return a.x*b.x+a.y*b.y;
}
double length(Vector a)
{
return sqrt(dot(a,a));
}
double angle(Vector a,Vector b)
{
return acos(dot(a,b))/length(a)/length(b);
}
double cross(Vector a,Vector b)
{
return a.x*b.y-a.y*b.x;
}
struct Circle
{
Point c;double x,y,r;
//Circle(Point c,double r):c(c),r(r) {}
Point point(double a)
{
return Point(c.x+cos(a)*r,c.y+sin(a)*r);
}
void read(){
scanf("%lf%lf%lf",&c.x,&c.y,&r);
x=c.x,y=c.y;
}
};
int getTangents(Circle A,Circle B,vector<Point> &p)
{
if(A.r<B.r) swap(A,B);
double d2=(A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);
double rdiff=A.r-B.r;
double base=atan2(B.y-A.y,B.x-A.x);
if(d2<rdiff*rdiff) return 0;
if(d2<eps&&dcmp(A.r-B.r)==0) return 0;
if(d2==rdiff*rdiff) return 0;
double ang=acos((A.r-B.r)/sqrt(d2));
p.push_back(A.point(base+ang));
p.push_back(B.point(base+ang));
p.push_back(A.point(base-ang));
p.push_back(B.point(base-ang));
return 1;
}
int ConvexHull(vector<Point> &p,Point *ch)
{
int n=(int)p.size();
sort(p.begin(),p.end());
int m=0;
for(int i=0;i<n;i++){
while(m>1&&cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
ch[m++]=p[i];
}
int k=m;
for(int i=n-2;i>=0;i--){
while(m>k&&cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
ch[m++]=p[i];
}
if(n>1) m--;
return m;
}
bool in(Point a,Point b,Circle c)
{
return dcmp(length(a-c.c)-c.r)==0&&(dcmp(length(b-c.c)-c.r))==0;
}
double getang(Point a)
{
return atan2(a.y,a.x);
}
const int maxn = 123;
Circle a[maxn];
Point ch[maxn<<4];
int n,m;
int main()
{
int t;cin>>t;
while(t--){
scanf("%d",&n);
for(int i=0;i<n;i++) a[i].read();
vector<Point> t,p;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++) getTangents(a[i],a[j],t);
}
for(Point i:t){
bool f=false;
for(int j=0;j<n;j++) if(length(a[j].c-i)+eps<a[j].r) f=true;
if(!f) p.push_back(i);
}
double ans=0.0;
m=ConvexHull(p,ch);ch[m]=ch[0];
if(m==0){
for(int i=0;i<n;i++) ans=max(ans,a[i].r);
printf("%.10f\n",ans*2*pi);continue;
}
for(int i=0;i<m;i++){
bool f=false;
for(int j=0;j<n&&!f;j++){
if(in(ch[i],ch[i+1],a[j])){
f=true;
double ang=getang(ch[i+1]-a[j].c)-getang(ch[i]-a[j].c);
while(ang<0) ang+=2*pi;
ans+=ang*a[j].r;
}
}
if(!f) ans+=length(ch[i]-ch[i+1]);
}
printf("%.10f\n",ans);
}
return 0;
}
H
题目描述
给定$n,k$,求最小的$y$使得$\forall x\in [1,n],gcd(x,y)=gcd(k,y)$,有$x=k$。
解题思路
首先必有$gcd(k,y)=k$,否则有$x=gcd(k,y)<k,s.t.gcd(x,y)=gcd(k,y)=x$。
故$y$为$k$的整数倍,$y=ak$。
又有$gcd(2k,y)!=k,gcd(3k,y)!=k,…,gcd(\lfloor\frac nk\rfloor k,y)!=k$。
故$2|a,3|a,4|a,…,\lfloor\frac nk\rfloor|a$,故$y=k\Pi_{p\in[2,\lfloor\frac nk\rfloor],p \in prime}p$。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def p(x):
if x<2:return False
for i in range(2,int(1+math.sqrt(x))):
if x%i==0:
return False
return True
t=int(input())
while(t):
t=t-1
n,k=map(int,input().split())
ans=k
for i in range(2,n+1):
if i*k>n:
break
if p(i):
ans=ans*i
print(ans)
I
题目描述
给一个数列$A$,有两种操作:
- 区间修改为$min(A_i,x)$
- 询问区间第$k$小
解题思路
暴力分块大法好.jpg
块内排好序,第一种操作相当于削头,每块一个标记$top$表示最大值不能超过多少,第二种操作枚举每块,块内二分查找即可。
要注意的地方在于,第一种操作的头尾两块遍历完要重新$sort$一遍。
单次询问复杂度:设块大小为$m$,第一种操作:$O(m+m\log m+\frac nm)$,第二种操作:$O(\frac nm\log m+m)$。取$m=\sqrt n$,总复杂度$O(\sqrt n \log n)$。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
typedef long long ll;
using namespace std;
int block,top[85010];
struct Ele{
int data,i;
bool operator<(const Ele &a)const{
return data<a.data;
}
bool operator==(const Ele &a)const{
return data==a.data;
}
}a[85010];
int l[85010],r[85010],flag;
int num(int L,int R,int x){
int lb=(L-1)/block+1,rb=(R-1)/block+1,i,ans=0;
for(i=(lb-1)*block+1;i<=(lb-1)*block+block;i++)
if(a[i].i>=L&&a[i].i<=R){
if(min(a[i].data,top[lb])==x)flag=1;
if(min(a[i].data,top[lb])<x)ans++;
}
if(lb!=rb)for(i=(rb-1)*block+1;i<=(rb-1)*block+block;i++)
if(a[i].i>=L&&a[i].i<=R){
if(min(a[i].data,top[rb])==x)flag=1;
if(min(a[i].data,top[rb])<x)ans++;
}
for(i=lb+1;i<rb;i++){
if(top[i]==x)flag=1;
if(top[i]<x)ans+=block;
else ans+=lower_bound(a+l[i],a+r[i]+1,(Ele){x,0})-a-l[i];
if(a[lower_bound(a+l[i],a+r[i]+1,(Ele){x,0})-a].data==x)flag=1;
}
return ans;
}
int main(){
int i,n,m;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d",&a[i].data),a[i].i=i;
block=sqrt(n);
memset(top,0x3f,sizeof(top));
for(i=1;r[i-1]!=n;i++){
l[i]=r[i-1]+1;
r[i]=min(n,l[i]+block-1);
sort(a+l[i],a+r[i]+1);
}
while(m--){
int opt,L,R,k;
scanf("%d%d%d%d",&opt,&L,&R,&k);
int lb=(L-1)/block+1,rb=(R-1)/block+1;
if(opt==1){
for(i=(lb-1)*block+1;i<=(lb-1)*block+block;i++)
if(a[i].i>=L&&a[i].i<=R)a[i].data=min(a[i].data,k);
sort(a+l[lb],a+r[lb]+1);
for(i=(rb-1)*block+1;i<=(rb-1)*block+block;i++)
if(a[i].i>=L&&a[i].i<=R)a[i].data=min(a[i].data,k);
sort(a+l[rb],a+r[rb]+1);
for(i=lb+1;i<rb;i++)
top[i]=min(top[i],k);
}else{
int bl=1,br=n,bm,res=1;
while(bl<br){
flag=0;
bm=(bl+br+1)/2;
if(num(L,R,bm)<k){
bl=bm;
if(flag)res=bl;
}
else br=bm-1;
}
printf("%d\n",res);
}
}
return 0;
}
J
题目描述
德州扑克?
解题思路
不太想补这个题,咕了
AC代码
2