| Solved | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9/12 | O | O | Ø | O | O | O | . | O | O | Ø | . | . |
- O for passing during the contest
- Ø for passing after the contest
- ! for attempted but failed
- · for having not attempted yet
A Xu Xiake in Henan Province
题目描述
输入四个数,分情况输出。
解题思路
签到,依题意做即可。
AC代码 - by Mogg
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
using namespace std;
typedef long long ll;
const int ms = 1e5 + 10;
const ll mod = 1000000007;
typedef pair<int, int> pt;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr);
int t;
cin >> t;
while (t--)
{
int a;
int len = 0;
for (int i = 0; i < 4; ++i)
{
cin >> a;
if (a > 0)len++;
}
switch (len)
{
case 0:
cout << "Typically Otaku\n";
break;
case 1:
cout << "Eye-opener\n";
break;
case 2:
cout << "Young Traveller\n";
break;
case 3:
cout << "Excellent Traveller\n";
break;
case 4:
cout << "Contemporary Xu Xiake\n";
}
}
return 0;
}
B Ultraman vs. Aodzilla and Bodzilla
题目描述
有两只怪兽,分别有$h_1,h_2$的血量和$a_1,a_2$的攻击力。每回合你可以选择一个怪兽进行攻击,第$i$回合你的攻击力是$i$。每回合怪兽如果没死会对你造成$a_i$点的伤害。
假设你在第$i$回合攻击第一只怪兽,$s[i]=’A’$,否则$s[i]=’B’$。于是得到一个攻击的$AB$序列,求在最小化受到伤害的同时最小化这个序列的字典序。
解题思路
首先,直接根据伤害血量百分比贪心的思路被
10 5 6 4这组数据否定。这组数据正确的攻击序列应为ABBAA。假设先把第一个怪兽打死。设$x$为一直打第一个怪兽直到它被打死所需的最少时间,有$\frac{x(x+1)}2\geq h_1$。设$y$为打两个怪兽且不浪费攻击力的情况下需要的最少时间,有$\frac{y(y+1)}2\geq h_1+h_2$。那么必然分别在这两个时间时把它们打死是最优的。现在只需要使得打第一只怪兽的时候尽量不浪费攻击力且使得字典序最小。
设$x$回合内一直攻击第一只怪兽浪费了$t$点攻击力,则必然能够用前$x$回合内的若干次攻击凑出$t$去攻击第二只怪兽,从而避免浪费。于是贪心地从高到低枚举攻击力分配给第二只怪兽即可。
当我们先把第二个怪兽打死时,类似的可以处理,但是因为要字典序最小,所以在贪心的时候需要从低到高枚举攻击力分配给第一只怪兽。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
typedef long long ll;
using namespace std;
char a[100010],b[100010];
ll ans1,ans2;
void calc(char a[],ll h1,ll a1,ll h2,ll a2,ll &ans){
int i;ll t1=sqrt(2*h1)-1,t2=sqrt(2*h1+2*h2)-1;
while(t1*(t1+1)/2<h1)t1++;
while(t2*(t2+1)/2<h1+h2)t2++;
ll tot=t1*(t1+1)/2-h1;
ll remain=h2-(t2*(t2+1)/2-t1*(t1+1)/2);
ans=1LL*a1*t1+1LL*a2*t2;
for(i=0;i<t1;i++)a[i]='B';
for(;i<t2;i++)a[i]='A';
a[i]='\0';
for(i=1;i<t1;i++){
if((remain-i<=0&&tot>=i)||tot-i>i){
a[i-1]='A';
tot-=i;
remain-=i;
}
}
if(tot)a[tot-1]='A';
}
void calc2(char a[],ll h1,ll a1,ll h2,ll a2,ll &ans){
int i;ll t1=sqrt(2*h1)-1,t2=sqrt(2*h1+2*h2)-1;
while(t1*(t1+1)/2<h1)t1++;
while(t2*(t2+1)/2<h1+h2)t2++;
ans=1LL*a1*t1+1LL*a2*t2;
for(i=0;i<t1;i++)a[i]='A';
for(;i<t2;i++)a[i]='B';
a[i]='\0';
ll remain=h2-(t2*(t2+1)/2-t1*(t1+1)/2);
ll now=t1*(t1+1)/2-h1;
while(remain>0&&t1){
if(now-t1>=0)now-=t1,remain-=t1,a[t1-1]='B';
t1--;
}
}
int main(){
int T;ll h1,h2,a1,a2;
scanf("%d",&T);
while(T--){
scanf("%lld%lld%lld%lld",&h1,&h2,&a1,&a2);
calc2(a,h1,a1,h2,a2,ans1);
calc(b,h2,a2,h1,a1,ans2);
if(ans1>ans2||(ans1==ans2&&strcmp(a,b)>0))printf("%lld %s\n",ans2,b);
else printf("%lld %s\n",ans1,a);
}
return 0;
}
C Supreme Command
题目描述
给一个$n\times n$的棋盘,上面有$n$个棋子,每一列、每一行上均有且只有一个棋子。
有$m$次操作:将棋盘上所有棋子向上/下/左/右移动$x$格,棋子可重叠,不可超出边界;询问某个点坐标;询问有多少对棋子在同一个格子上。
$1\leq n,m\leq 300000$
解题思路
考虑将边界向内收,用四个变量
lrud记录上下左右收到哪里了,用另四个变量LRUD记录空出来的区域大小。(现在看来似乎只用后四个就行了)
记录收起来的左上角、右上角、左下角、右下角的棋子个数(代码中使用了$cnt[1],cnt[3],cnt[7],cnt[9]$,因为刚开始的时候是当做九宫格处理的,后来发现只需要维护这四个即可),因为只有在这里相遇。然后每个点只能使用一次,记录一下即可。
调了好久结果是一个$mplr$写成$mpud$的问题……
这题没有一个中强的数据,提供一个:
1 | 1 |
答案是0 0 0 1 2 10。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
typedef long long ll;
using namespace std;
int mplr[N],mpud[N],mark[N],cnt[15];
int used[N];
pair<int,int>p[N];
ll f(int x){return 1LL*x*(x-1)/2;}
ll calc(int l,int r,int u,int d){
if(l==r&&u==d)return f(cnt[1]+cnt[3]+cnt[7]+cnt[9]);
else if(l==r)return f(cnt[1]+cnt[3])+f(cnt[7]+cnt[9]);
else if(u==d)return f(cnt[1]+cnt[7])+f(cnt[3]+cnt[9]);
return f(cnt[1])+f(cnt[3])+f(cnt[7])+f(cnt[9]);
}
int main(){
int i,T,n,m;
scanf("%d",&T);
while(T--){
memset(used,0,sizeof(used));
memset(mark,0,sizeof(mark));
memset(cnt,0,sizeof(cnt));
memset(mplr,0,sizeof(mplr));
memset(mpud,0,sizeof(mpud));
scanf("%d%d",&n,&m);
int l=1,r=n,u=1,d=n;
int L=0,R=0,U=0,D=0;
for(i=1;i<=n;i++){
scanf("%d%d",&p[i].fi,&p[i].se);
mpud[p[i].fi]=mplr[p[i].se]=i;
if(p[i].fi==1){
if(p[i].se==1)cnt[1]++,used[i]=1;
else if(p[i].se==n)cnt[3]++,used[i]=1;
}else if(p[i].fi==n){
if(p[i].se==1)cnt[7]++,used[i]=1;
else if(p[i].se==n)cnt[9]++,used[i]=1;
}
}
while(m--){
int x;char opt[3]={0};
scanf("%s",opt);
if(opt[0]!='!')scanf("%d",&x);
if(opt[0]=='L'){
if(L>x)L-=x,R+=x,x=0;
else x-=L,R+=L,L=0;
while(x--&&l<r){
if(used[mplr[l+1]]);
else if(p[mplr[l+1]].first<=u)cnt[1]++,used[mplr[l+1]]=1;
else if(p[mplr[l+1]].first>=d)cnt[7]++,used[mplr[l+1]]=1;
l++;R++;
}
}else if(opt[0]=='R'){
if(R>x)R-=x,L+=x,x=0;
else x-=R,L+=R,R=0;
while(x--&&l<r){
if(used[mplr[r-1]]);
else if(p[mplr[r-1]].first<=u)cnt[3]++,used[mplr[r-1]]=1;
else if(p[mplr[r-1]].first>=d)cnt[9]++,used[mplr[r-1]]=1;
r--;L++;
}
}else if(opt[0]=='U'){
if(U>x)U-=x,D+=x,x=0;
else x-=U,D+=U,U=0;
while(x--&&u<d){
if(used[mpud[u+1]]);
else if(p[mpud[u+1]].second<=l)cnt[1]++,used[mpud[u+1]]=1;
else if(p[mpud[u+1]].second>=r)cnt[3]++,used[mpud[u+1]]=1;
u++;D++;
}
}else if(opt[0]=='D'){
if(D>x)D-=x,U+=x,x=0;
else x-=D,U+=D,D=0;
while(x--&&u<d){
if(used[mpud[d-1]]);
else if(p[mpud[d-1]].second<=l)cnt[7]++,used[mpud[d-1]]=1;
else if(p[mpud[d-1]].second>=r)cnt[9]++,used[mpud[d-1]]=1;
d--;U++;
}
}else if(opt[0]=='?')printf("%d %d\n",min(d,max(u,p[x].fi))-u+1+U,min(r,max(l,p[x].se))-l+1+L);
else printf("%lld\n",calc(l,r,u,d));
}
}
return 0;
}
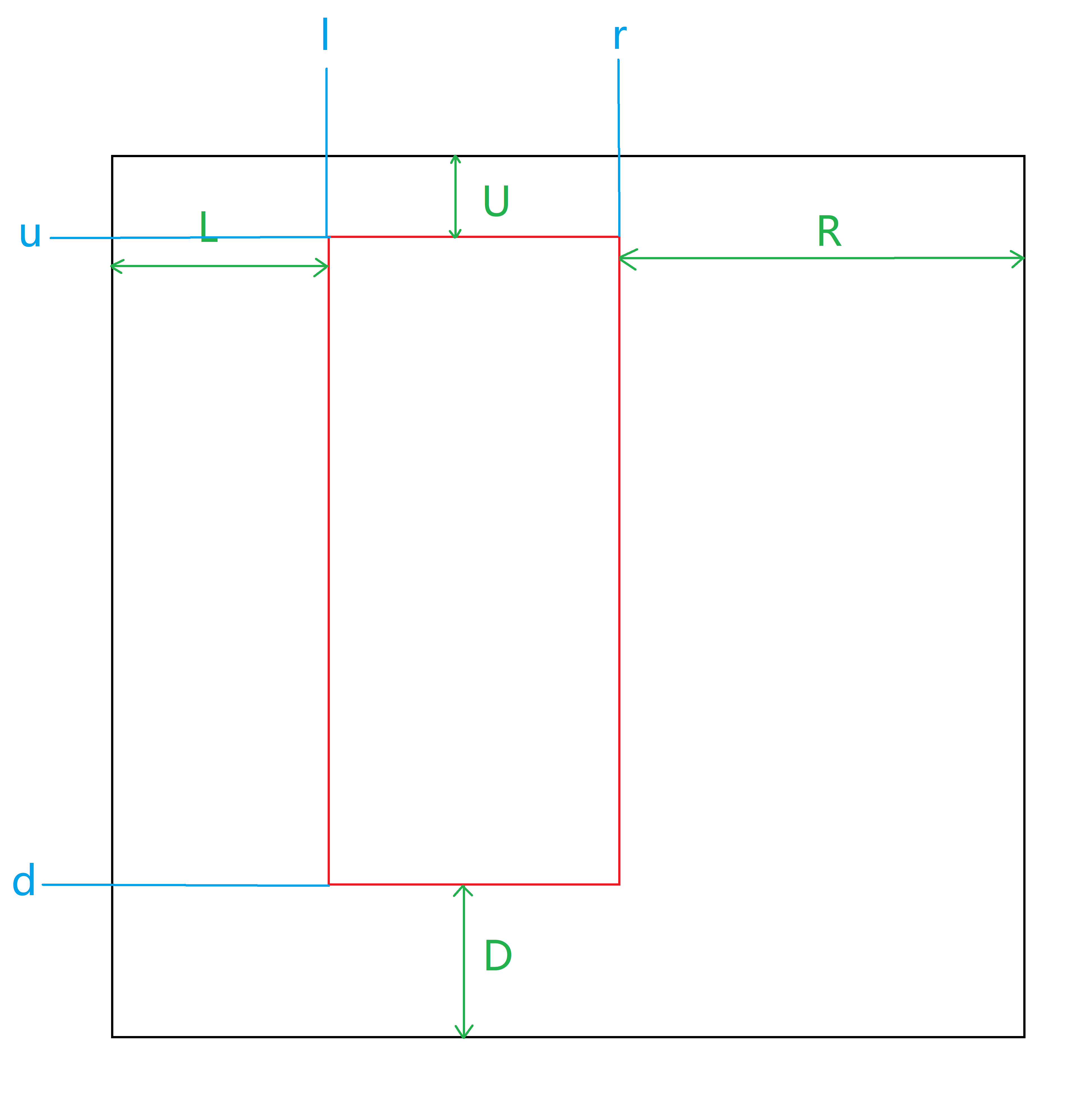
D Keiichi Tsuchiya the Drift King
题目描述
有一辆矩形的车,从直道行驶到一个圆环弧形轨道,要求车时刻与内侧轨道相切,给定车的边长、圆环内半径和圆环的弧度,求圆环宽度最大值。
解题思路
根据弧度,分两种情况讨论:在直道上取得最大值,在弧上取得最大值。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
typedef long long ll;
using namespace std;
int main(){
int T,a,b,r,d;
scanf("%d",&T);
while(T--){
scanf("%d%d%d%d",&a,&b,&r,&d);
double theta=d/360.0*2.0*acos(-1);
double bound=atan2(b,a+r),w;
if(theta>bound)w=sqrt(b*b+(a+r)*(a+r));
else w=b*sin(theta)+(a+r)*cos(theta);
printf("%.12f\n",w-r);
}
return 0;
}
E Resistors in Parallel
题目描述
有$n$个电阻,定义第$i$个电阻的阻值$R_i$为:$i$,当且仅当$i$不能被某个数的平方整除;否则为$0$。
定义一个编号为$i$的电阻集合的阻值为所有$i$的因数$j$对应的电阻$R_j$并联产生的阻值。
给定$n$,求编号为$1\leq x\leq n$的电阻集合的最小阻值。$1\leq n\leq 10^{100}$。
解题思路
$R=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_k}}$
最大化分母:尽量选小的数($\frac 12,\frac 13,\frac 15,\frac 17…,\frac 1{2\times 3},\frac 1{2\times 5},\frac 1{3\times 5},\frac1{2\times 3\times 5}…$)
容易看出,当$n$选择为前$p$个质数的乘积的时候是最优的,答案可以通过大数+前缀和求出。
AC代码 - by Mogg
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
ms = 100000
phi = [False for i in range(ms)]
pri = []
cnt = 0
def init():
global cnt
phi[1] = True
for i in range(2,ms):
if not phi[i]:
pri.append(i)
cnt += 1
j = 0
while j< cnt and i*pri[j]<ms :
phi[i*pri[j]] = True
if i%pri[j] == 0:
break
j += 1
def gcd(a,b):
if(a == 0):
return b
return gcd(b%a,a)
def solve(x):
up = 1
low = 1
for i in range(cnt):
if up*pri[i] > x:
break
up*=pri[i]
low = (pri[i] + 1)*(low)
g = gcd(up,low)
print(str(up//g) + "/" + str(low//g))
init()
t = int(input())
for i in range(t):
solve(int(input()))
F Honeycomb
题目描述
字符串的形式输入一个蜂巢,求$S,T$之间的最短距离。
解题思路
非常暴力(麻烦)的求出各个孔的位置和连通性,$bfs$一下即可。
AC代码 - by Mogg
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
using namespace std;
typedef long long ll;
const int ms=1e3+10;
const ll mod=1000000007;
typedef pair<int,int>pt;
vector<int>g[ms*ms];
vector<pt>p0={{3,1},{1,3},{1,7},{3,9},{5,7},{5,3},{3,1}};
vector<pt>p1={{5,7},{3,9},{3,13},{5,15},{7,13},{7,9},{5,7}};
vector<pt>p2={{0,-1},{-1,0},{0,1},{1,1},{1,0},{1,-1}};
vector<pt>p3={{-1,-1},{-1,0},{-1,1},{0,1},{1,0},{0,-1}};
pt b0={3,5},b1={5,11};
char s[ms*4][ms*6];
int r,c;
int po(int x,int y){
return c*(x-1)+y;
}
bool vis[ms*ms];
int dij(int begin,int end){
for(int i=1;i<=r*c;++i)vis[i]=false;
queue<pt>q;
q.push({begin,0});
vis[begin]=true;
while(!q.empty()){
int x=q.front().first,y=q.front().second;q.pop();
for(int i:g[x]){
if(vis[i]) continue;
vis[i]=true;
if(i==end) return y+2;
q.push({i,y+1});
}
}
return -1;
}
int main(){
ios::sync_with_stdio(false);cin.tie(nullptr);
int t;
cin>>t;
while(t--){
cin>>r>>c;
vector<pt>tmp;
cin.getline(s[0]+1,6*c+5);
for(int i=1;i<=4*r+3;++i)cin.getline(s[i]+1,6*c+5);
for(int i=1;i<=r*c;++i)g[i].clear();
int begin=0,end=0;
for(int i=1;i<=r;++i){
for(int j=1;j<=c;++j){
int h=(i-1)*4,v=(j-1)/2*12;
if(j&1){
if(s[b0.first+h][b0.second+v]=='S') begin=po(i,j);
else if(s[b0.first+h][b0.second+v]=='T') end=po(i,j);
for(int k=0;k<6;++k){
pt t1={p0[k].first+h,p0[k].second+v};
pt t2={p0[k+1].first+h,p0[k+1].second+v};
pt mid={(t1.first+t2.first)/2,(t1.second+t2.second)/2};
if(s[mid.first][mid.second]==' '){
g[po(i,j)].push_back(po(i+p3[k].first,j+p3[k].second));
g[po(i+p3[k].first,j+p3[k].second)].push_back(po(i,j));
}
}
}
else{
if(s[b1.first+h][b1.second+v]=='S') begin=po(i,j);
else if(s[b1.first+h][b1.second+v]=='T') end=po(i,j);
for(int k=0;k<6;++k){
pt t1={p1[k].first+h,p1[k].second+v};
pt t2={p1[k+1].first+h,p1[k+1].second+v};
pt mid={(t1.first+t2.first)/2,(t1.second+t2.second)/2};
if(s[mid.first][mid.second]==' '){
g[po(i,j)].push_back(po(i+p2[k].first,j+p2[k].second));
g[po(i+p2[k].first,j+p2[k].second)].push_back(po(i,j));
}
}
}
}
}
cout<<dij(begin,end)<<"\n";
}
return 0;
}
G Shortest Paths on Random Forests
题目描述
解题思路
AC代码
2
H Can You Solve the Harder Problem?
题目描述
定义$Q(l,r)=max_{l\leq i\leq r}a_i$,两个区间是本质相同的当且仅当这两个区间长度相同且对应数相同(如$1,2,1,2$中,$[1,2][3,4]$两个区间即为本质相同的区间),求出本质不同的区间$Q$之和。
$1\leq a_i\leq 10^6,1\leq n\leq 2\times 10^5$。
解题思路
一看到本质不同瞬间想到后缀自动机、后缀数组的问题。显然,$a_i$太大,用后缀自动机不好建树,于是考虑使用后缀数组。
首先将离散化的$a$扔到后缀数组中求出$sa,height$两个所需数组(没离散化$T$了无数发)。
考虑先计算出所有区间的总和,再去掉重叠区间的贡献。
总和可以通过单调栈计算出每一个数向右最近的比它大的数的位置,然后从后向前递推计算出以$i$开头的所有区间$Q$之和$cost_i$。
重叠区间贡献可以枚举后缀数组中相邻两个串的$lcp$,即为$h_i$。这个$h_i$对应下标分别为$sa_{i-1}$和$sa_{i}$开始的后缀,不妨只看$sa_i$中的贡献,即以$sa_i$为左端点、右端点在$[sa_i,sa_i+h_i]$区间内的所有区间的$Q$之和。假设在$sa_i$右边、$sa_i+h_i$左边的最右端的比$a_{sa_i}$大的数位置在$pos$,那么很容易得出$[pos,sa_i+h_i]$区间的贡献为$a_{pos}\times (sa_i+h_i-pos+1)$(这个区间内最大的数均为$a_{pos}$)。这个$pos$可以通过单调栈求出的$r_i$数组进行倍增的预处理求出来,而$[sa_i,pos-1]$的贡献即为$cost_{sa_i}-cost_{pos}$,而这已经被求出来了。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
typedef long long ll;
using namespace std;
using namespace std;
typedef long long ll;
int s[N];
int n,sa[N],c[N],x[N],y[N];
int lsh[N];
void getsa(){
int i,k,m;
for(i=1;i<=n;i++)c[i]=s[i];
sort(c+1,c+1+n);
m=unique(c+1,c+1+n)-c;
for(i=1;i<=n;i++)x[i]=lower_bound(c+1,c+m,s[i])-c;
for(i=0;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[x[i]]++;
for(i=1;i<=m;i++)c[i]+=c[i-1];
for(i=n;i;i--)sa[c[x[i]]--]=i;
for(k=1;k<=n;k<<=1){
int p=0;
for(i=n-k+1;i<=n;i++)y[++p]=i;
for(i=1;i<=n;i++)if(sa[i]>k)y[++p]=sa[i]-k;
for(i=0;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[x[y[i]]]++;
for(i=1;i<=m;i++)c[i]+=c[i-1];
for(i=n;i;i--)sa[c[x[y[i]]]--]=y[i];
swap(x,y);
p=x[sa[1]]=1;
for(i=2;i<=n;i++)
x[sa[i]]=y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]?p:++p;
if(p>=n)break;
m=p;
}
}
int h[N],rnk[N];
void geth(){
int i,j,k=0;
for(i=1;i<=n;i++)rnk[sa[i]]=i;
for(i=1;i<=n;i++){
if(k)k--;
j=sa[rnk[i]-1];
while(s[i+k]==s[j+k])k++;
h[rnk[i]]=k;
}
}
int sta[N],top,r[N];
int fa[22][N];
ll cost[N];//cost start from i to r-end
int main(){
int i,j,T;
scanf("%d",&T);
while(T--){
ll ans=0;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&s[i]);
getsa();
geth();
top=0;
for(i=1;i<=n;i++){
while(top&&s[sta[top]]<s[i]){
r[sta[top]]=fa[0][sta[top]]=i;
top--;
}
sta[++top]=i;
}
while(top)r[sta[top]]=fa[0][sta[top]]=n+1,top--;
r[n+1]=fa[0][n+1]=n+1;
for(i=1;i<20;i++){
if((1LL<<i)<=n)for(j=1;j<=n;j++)fa[i][j]=fa[i-1][fa[i-1][j]];
else for(j=1;j<=n;j++)fa[i][j]=n+1;
}
cost[n+1]=0;
for(i=n;i>=1;i--)cost[i]=cost[r[i]]+1LL*(r[i]-i)*s[i],ans+=cost[i];
for(i=2;i<=n;i++){
int left=sa[i],now=left;
if(!h[i])continue;
for(j=20;j>=0;j--)
if(fa[j][now]&&fa[j][now]<=left+h[i])now=fa[j][now];
ans-=1LL*(left+h[i]-now)*s[now];
ans-=1LL*(cost[sa[i]]-cost[now]);
}
printf("%lld\n",ans);
}
return 0;
}
I Distance
题目描述
有一堆点,分别求出$2\leq k\leq n$的时候,选择$k$个点,使得两两间距离之和最大,这个最大值。
解题思路
每次选择最外层两个点即可。
AC代码 - by qxforever
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
typedef long long ll;
const int maxn = 1e5+23;
int T,n;
int a[maxn];
int p[maxn];
int main()
{
cin >> T;
while(T--){
scanf("%d",&n);
p[1]=0;
for(int i=2;i<=n;i++) scanf("%d",a+i),p[i]=p[i-1]+a[i];
int i,j;ll ans=0,dis=0;
for(i=1,j=n;i<=j;i++,j--){
ans+=dis;
printf("%lld%c",ans,i!=j?' ':'\n');
if(i!=j){
ans+=dis;
ans+=p[j]-p[i];
dis+=(p[j]-p[i]);
printf("%lld%c",ans,j-i>1?' ':'\n');
}
}
}
}
J Carpets Removal
题目描述
$m\times m$的矩形地板,上面乱七八糟铺了$n$块可以相互重叠的矩形地毯。问选择两块地毯移走后,剩下还被地毯覆盖的格子最少有多少。
解题思路
首先,很显然用二维前缀和维护一下每个点上有几个毯子,只考虑有一个或两个的情况。
记录下每一块毯子独立拿走后减少的格子数$cnt_i$(即只被这一种地毯覆盖的格子数),那么两块地毯的贡献就是$cnt_i+cnt_j+s$,$s$表示只被这两块地毯同时覆盖的格子数。
当$s=0$时,直接取$cnt$数组里的最大次大值加起来即可。
这里用到一个极为巧妙的算法:
二维前缀和可以维护每个点被几个毯子覆盖,但其实同时也可以维护被覆盖的编号之和,而这个编号之和在被覆盖个数为$1$的时候即为这个点对应的编号,为$2$的时候即为这个点对应的两个编号$x+y$。那么再维护一个被覆盖的编号的平方之和,这样就可以维护出$x^2+y^2$了。有了$x+y,x^2+y^2$,就能求出$x,y$了。
于是$s\neq 0$时,枚举每一个这样的$(x,y)$对即可得到答案。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
typedef long long ll;
using namespace std;
ll s[M][M],s2[M][M],cnt[M][M];
int num[N];
map<int,int>f1;
map<pair<int,int>,int>f2;
int main(){
int i,j,T,n,m;
scanf("%d",&T);
while(T--){
ll ans=0,tot=0;
scanf("%d%d",&n,&m);
for(i=0;i<=m;i++)for(j=0;j<=m;j++)cnt[i][j]=s[i][j]=s2[i][j]=0;
memset(num,0,sizeof(int)*(n+1));
f1.clear();f2.clear();
for(i=0;i<n;i++){
int x,y,a,b;
scanf("%d%d%d%d",&a,&x,&b,&y);
cnt[a][b]++;cnt[x+1][b]--;cnt[a][y+1]--;cnt[x+1][y+1]++;
s[a][b]+=i;s[x+1][b]-=i;s[a][y+1]-=i;s[x+1][y+1]+=i;
s2[a][b]+=1LL*i*i;s2[x+1][b]-=1LL*i*i;s2[a][y+1]-=1LL*i*i;s2[x+1][y+1]+=1LL*i*i;
}
for(i=1;i<=m;i++){
for(j=1;j<=m;j++){
cnt[i][j]+=cnt[i-1][j]+cnt[i][j-1]-cnt[i-1][j-1];
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
s2[i][j]+=s2[i-1][j]+s2[i][j-1]-s2[i-1][j-1];
if(cnt[i][j])tot++;
if(cnt[i][j]==1){
num[s[i][j]]++;
f1[s[i][j]]++;
}else if(cnt[i][j]==2){
int x,y,xminusy=sqrt(2*s2[i][j]-s[i][j]*s[i][j]);
x=(xminusy+s[i][j])/2;y=s[i][j]-x;
if(x>y)swap(x,y);
f2[mp(x,y)]++;
}
}
}
for(auto i:f2)ans=max(ans,(ll)i.se+num[i.fi.fi]+num[i.fi.se]);
ll mx=0,se=0;
for(auto i:f1){
if(i.se>mx)se=mx,mx=i.se;
else if(i.se>se)se=i.se;
}
ans=max(ans,mx+se);
printf("%lld\n",tot-ans);
}
return 0;
}
K Counting Failures on a Trie
题目描述
解题思路
AC代码
2
L Connected Subgraphs
题目描述
解题思路
AC代码
2