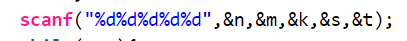| Solved | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7/11 | O | Ø | O | O | . | . | . | . | Ø | O | O |
- O for passing during the contest
- Ø for passing after the contest
- ! for attempted but failed
- · for having not attempted yet
A
题目描述
给一个点数为$n$的树,树上有$k$个人在不同的节点上,他们每秒能走一条边,问他们集会(走到相同位置)最短需要多少时间。
解题思路
先把树转化成叶子节点均为人的新树,在新树上求直径即可。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
typedef long long ll;
using namespace std;
int n,k,a,b;
vector<int>G[N],G2[N];
int inG2[N];
int dfs(int x,int f){
int i;
for(i=0;i<G[x].size();i++){
int y=G[x][i];
if(y!=f&&dfs(y,x)){
inG2[x]++;
G2[x].push_back(y);
G2[y].push_back(x);
}
}
return inG2[x];
}
int ans=0,d[N],vis[N];
void dp(int x){
int i;
vis[x]=1;
for(i=0;i<G2[x].size();i++){
int y=G2[x][i];
if(!vis[y]){
dp(y);
ans=max(ans,d[x]+d[y]+1);
d[x]=max(d[x],d[y]+1);
}
}
}
int main(){
int i;
scanf("%d%d",&n,&k);
for(i=1;i<n;i++){
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);
}
for(i=0;i<k;i++)
scanf("%d",&a),inG2[a]++;
int rt=1;while(!inG2[rt])rt++;
dfs(rt,-1);
dp(rt);
printf("%d",(ans+1)/2);
return 0;
}
B
题目描述
$n$个集合,$m$次询问,每次询问一个区间$[l,r]$,问是否任意区间中的集合都能用异或表示$x$。
$1\leq n,m\leq 50000,0\leq x<2^{32}$。
解题思路
线性基+线段树。
线性基求交的思想很有意思,本质就是线性空间的两组基求交,比如两平面求交。
假设现在我们要对$a,b$两组基求交。从低到高枚举$b$的基$b_i$,如果它能够被$a$和以前枚举出的$b$($b_1…b_{i-1}$)线性表示,假设$b_i=a_{k_1}\oplus a_{k_2}\oplus…\oplus a_{k_p}\oplus b_{l_1}\oplus b_{l_2}\oplus…\oplus b_{l_q}$,则$a_{k_1}\oplus a_{k_2}\oplus…\oplus a_{k_p}$为交集的一个基。故维护一个$tot$代表$a$和以前的$b$组成的基,维护一个到达$tot_j$所需要的$a_{k_1}\oplus a_{k_2}\oplus…\oplus a_{k_p}$的值,每次插入$b_i$时分别异或插入即可。
每次合并复杂度$O(32^2)$,建立线段树复杂度$O(32^2n\log n)$,每次询问$O(32\log n)$,总时间复杂度$O(32^2n\log n+32m\log n)$。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
typedef long long ll;
using namespace std;
struct Base{
int a[33];
}t[N<<2];
int n,m;
int insert(Base *bas,int x,int flag){//flag:是否真插入
int i;
for(i=31;i>=0;i--){
if((1<<i)&x){
if((*bas).a[i])x^=(*bas).a[i];
else{
if(flag)(*bas).a[i]=x;
return 1;
}
}
if(!x)return 0;
}
return printf("err"),0;
}
void merge(Base *e,Base a,Base b){
Base tot;
int i,j;
for(i=0;i<32;i++)tot.a[i]=a.a[i],(*e).a[i]=0;
for(i=0;i<32;i++){
if(b.a[i]){
int cur=b.a[i],add=0;
for(j=i;j>=0;j--){
if((1<<j)&cur){
if(tot.a[j]){
cur^=tot.a[j];
add^=a.a[j];
if(!cur){
(*e).a[i]=add;
break;
}
}else{
tot.a[j]=cur;
a.a[j]=add;
break;
}
}
}
}
}
}
int siz[N],v[N][M];
void build(int p,int l,int r){
if(l==r){
int i;
for(i=0;i<siz[l];i++)insert(&t[p],v[l][i],1);
return;
}
build(p<<1,l,(l+r)>>1);
build(p<<1|1,((l+r)>>1)+1,r);
merge(&t[p],t[p<<1],t[p<<1|1]);
}
int query(int p,int l,int r,int ql,int qr,int x){
if(ql<=l&&qr>=r)return !insert(&t[p],x,0);
if(ql<=(l+r)>>1&&!query(p<<1,l,(l+r)>>1,ql,qr,x))return 0;
if(qr>((l+r)>>1)&&!query(p<<1|1,((l+r)>>1)+1,r,ql,qr,x))return 0;
return 1;
}
int main(){
int i,j;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++){
scanf("%d",&siz[i]);
for(j=0;j<siz[i];j++)scanf("%d",&v[i][j]);
}
build(1,1,n);
for(i=0;i<m;i++){
int l,r,x;
scanf("%d%d%d",&l,&r,&x);
printf("%s\n",query(1,1,n,l,r,x)?"YES":"NO");
}
return 0;
}
C
题目描述
给两个数列$a_i,b_i$,求$max(min(a_{l…r})\times sum(b_{l…r}))$。
解题思路
分治,对每一个$[l,r]$对最小值分治,找到向左右延伸的$b$前缀和最大最小值更新答案即可。
首先,我用$ST$表,获得了$MLE$ 。
MLE代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
typedef long long ll;
using namespace std;
int n;
ll a[N],b[N];
int rmq[22][N];
int rmin[22][N],rmax[22][N];
int lg[N];
ll ans=-1e18;
void init(int rmq[][N],ll *a,int flag){
int i,j;
for(i=0;i<=n;i++)rmq[0][i]=i;
for(j=1;(1<<j)<=n;j++){
for(i=0;i+(1<<(j-1))-1<=n;i++){
if(flag==1){//max
if(a[rmq[j-1][i]]<a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}else{//min
if(a[rmq[j-1][i]]>a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}
}
}
}
int query(int rmq[][N],ll *a,int l,int r,int flag){
int f=lg[r-l+1];
if(flag){
if(a[rmq[f][l]]<a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}else{
if(a[rmq[f][l]]>a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}
}
void dc(int l,int r){
if(l>r)return;
if(l==r){
ans=max(ans,a[l]*(b[l]-b[l-1]));
return;
}
int pos=query(rmq,a,l,r,0);
if(a[pos]<0){
ans=max(ans,a[pos]*(b[query(rmin,b,pos,r,0)]-b[query(rmax,b,l-1,pos,1)]));
}else{
ans=max(ans,a[pos]*(b[query(rmax,b,pos,r,1)]-b[query(rmin,b,l-1,pos,0)]));
}
dc(l,pos-1);
dc(pos+1,r);
}
int main(){
int i;
scanf("%d",&n);
for(i=2;i<N;i++)lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);
for(i=1;i<=n;i++)scanf("%lld",&a[i]);
for(i=1;i<=n;i++)scanf("%lld",&b[i]),b[i]+=b[i-1];
init(rmq,a,0);
init(rmin,b,0);
init(rmax,b,1);
dc(1,n);
printf("%lld",ans);
return 0;
}
有点自闭,把$ST$表换成笛卡尔树试了试。
获得了$TLE$ 。
TLE代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
typedef long long ll;
using namespace std;
int n;
ll a[N],b[N];/*
int rmq[24][N];
int rmin[24][N],rmax[24][N];
int lg[N];*/
int rt1,rtmin,rtmax;
int ls[3][N],rs[3][N],fa[3][N];
ll ans=-1e18;/*
void init(int rmq[][N],ll *a,int flag){
int i,j;
for(i=0;i<=n;i++)rmq[0][i]=i;
for(j=1;(1<<j)<=n;j++){
for(i=0;i+(1<<(j-1))-1<=n;i++){
if(flag==1){//max
if(a[rmq[j-1][i]]<a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}else{//min
if(a[rmq[j-1][i]]>a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}
}
}
}*/
int init(int *ls,int *rs,int *fa,ll *a,int flag){
stack<int> st; //存放节点的key值
int rt,last;
for(int i=0;i<=n;++i){
last=-1;
while(!st.empty()){
if(a[st.top()]<a[i]&&!flag||flag&&a[st.top()]>a[i]){
rt=st.top();
if(rs[rt]){
fa[rs[rt]]=i;
ls[i]=rs[rt];
}
rs[rt]=i;
fa[i]=rt;
break;
}
last=st.top(); st.pop();
}
if(st.empty()&&last){
fa[last]=i;
ls[i]=last;
}
st.push(i);
}
while(!st.empty())rt=st.top(), st.pop();
return rt;
}
int query(int *ls,int *rs,int root,int l,int r){
while(root<l||root>r)root=root<l?rs[root]:ls[root];
return root;
}
/*
int query(int rmq[][N],ll *a,int l,int r,int flag){
int f=lg[r-l+1];
if(flag){
if(a[rmq[f][l]]<a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}else{
if(a[rmq[f][l]]>a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}
}*/
void dc(int l,int r){
if(l>r)return;
if(l==r){
ans=max(ans,a[l]*(b[l]-b[l-1]));
return;
}
int pos=query(ls[0],rs[0],rt1,l,r);
//int pos=query(rmq,a,l,r,0);
/*if(a[pos]<0){
ans=max(ans,a[pos]*(b[query(rmin,b,pos,r,0)]-b[query(rmax,b,l-1,pos,1)]));
}else{
ans=max(ans,a[pos]*(b[query(rmax,b,pos,r,1)]-b[query(rmin,b,l-1,pos,0)]));
}*/
if(a[pos]<0){
ans=max(ans,a[pos]*(b[query(ls[1],rs[1],rtmin,pos,r)]-b[query(ls[2],rs[2],rtmax,l-1,pos)]));
}else{
ans=max(ans,a[pos]*(b[query(ls[2],rs[2],rtmax,pos,r)]-b[query(ls[1],rs[1],rtmin,l-1,pos)]));
}
dc(l,pos-1);
dc(pos+1,r);
}
int main(){
int i;
scanf("%d",&n);
//for(i=2;i<N;i++)lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);
for(i=1;i<=n;i++)scanf("%lld",&a[i]);
for(i=1;i<=n;i++)scanf("%lld",&b[i]),b[i]+=b[i-1];
rt1=init(ls[0],rs[0],fa[0],a,0);
rtmin=init(ls[1],rs[1],fa[1],b,0);
rtmax=init(ls[2],rs[2],fa[2],b,1);
dc(1,n);
printf("%lld",ans);
return 0;
}
学习了一发单调栈求最小值影响范围的,把最初的代码改了一下优化成两个$ST$表,恰好卡住$510M$,但莫名其妙$WA$了,对着标程各种数据拍了好久没找出问题,留坑准备拿到数据后再查一下。
WA代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
typedef long long ll;
using namespace std;
int n;
int a[N];ll b[N];
int rmin[23][N],rmax[23][N];
int lg[N];
ll ans=-1e18;
void init(int rmq[][N],ll *a,int flag){
int i,j;
for(i=0;i<=n;i++)rmq[0][i]=i;
for(j=1;(1<<j)<=n;j++){
for(i=0;i+(1<<(j-1))-1<=n;i++){
if(flag==1){//max
if(a[rmq[j-1][i]]<a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}else{//min
if(a[rmq[j-1][i]]>a[rmq[j-1][i+(1<<(j-1))]])
rmq[j][i]=rmq[j-1][i+(1<<(j-1))];
else rmq[j][i]=rmq[j-1][i];
}
}
}
}
int query(int rmq[][N],ll *a,int l,int r,int flag){
int f=lg[r-l+1];
if(flag){
if(a[rmq[f][l]]<a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}else{
if(a[rmq[f][l]]>a[rmq[f][r+1-(1<<f)]])return rmq[f][r+1-(1<<f)];
else return rmq[f][l];
}
}
int sta[N],top=1,c[N][2];
void dc(int pos,int l,int r){
int L=c[pos][0],R=c[pos][1];
if(!pos||l>r)return;
if(a[pos]<0){
ans=max(ans,a[pos]*(b[query(rmin,b,pos,r,0)]-b[query(rmax,b,l-1,pos-1,1)]));
}else if(a[pos]>0){
ans=max(ans,a[pos]*(b[query(rmax,b,pos,r,1)]-b[query(rmin,b,l-1,pos-1,0)]));
}else ans=max(ans,0LL);
if(L)dc(L,l,pos-1);
if(R)dc(R,pos+1,r);
}
int main(){
int i;
//freopen("data.in","r",stdin);
scanf("%d",&n);
for(i=2;i<N;i++)lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)scanf("%lld",&b[i]),b[i]+=b[i-1];
sta[1]=1;
for(i=2;i<=n;i++){
while(top&&a[i]<a[sta[top]]){
c[sta[top]][1]=c[i][0];
c[i][0]=sta[top];
top--;
}
sta[++top]=i;
}
while(top>1)c[sta[top-1]][1]=sta[top--];
init(rmin,b,0);
init(rmax,b,1);
dc(sta[1],1,n);
printf("%lld",ans);
return 0;
}
好耶,这是不想让我过了。那考虑一下标程的思路,每次在分治的过程中处理好左右端的最大最小值,感觉十分巧妙。
$upd$:
注释部分…是一个故事,算了不讲了
然后把上面$WA$的代码注释部分改一遍就变成了$MLE$……
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
typedef long long ll;
using namespace std;
int sta[N],top,a[N],tree[N][2];
ll b[N],ans=-1e18;
struct Datamax{
ll pre,suf,sum;
friend Datamax operator +(const Datamax &l,const Datamax &r){
ll sf=max(l.suf+r.sum,r.suf);
ll s=l.sum+r.sum;
ll p=max(l.sum+r.pre,l.pre);
return (Datamax){p,sf,s};
}
}mx[N];
Datamax fmx(ll x){
ll p=max(x,0LL);
ll sf=max(x,0LL);
ll s=x;
return (Datamax){p,sf,s};
}
struct Datamin{
ll pre,suf,sum;
friend Datamin operator +(const Datamin &l,const Datamin &r){
ll sf=min(l.suf+r.sum,r.suf);
ll s=l.sum+r.sum;
ll p=min(l.sum+r.pre,l.pre);
return (Datamin){p,sf,s};
}
}mn[N];
Datamin fmn(ll x){
ll p=min(x,0LL);
ll sf=min(x,0LL);
ll s=x;
return (Datamin){p,sf,s};
}
void dc(int x){
int l=tree[x][0],r=tree[x][1];
if(l)dc(l);
if(r)dc(r);
ans=max(ans,a[x]*(mx[l].suf+b[x]+mx[r].pre));
ans=max(ans,a[x]*(mn[l].suf+b[x]+mn[r].pre));
mx[x]=mx[l]+fmx(b[x])+mx[r];
mn[x]=mn[l]+fmn(b[x])+mn[r];
}
int main(){
int i,n;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)scanf("%lld",&b[i]);
sta[1]=top=1;
for(i=2;i<=n;i++){
while(top&&a[i]<a[sta[top]]){
tree[sta[top]][1]=tree[i][0];
tree[i][0]=sta[top];
top--;
}
sta[++top]=i;
}
while(top>1)tree[sta[top-1]][1]=sta[top],top--;//......
dc(sta[1]);
printf("%lld",ans);
return 0;
}
D
题目描述
给一个$n$,求$3$的倍数数列$x_i$使得$|_ix_i=n$(或和为$n$),并最小化数列长度。
解题思路
如果$n$为$3$的倍数,直接输出$n$
否则通过观察,二进制对$3$的余数满足$12121212…$,故$n$的二进制必然为三个或以上个$1$。
分类讨论:当$n%3=1$时,如果有两个余数为$1$的位$p,q$,则答案可以为$n-p,n-q$;如果只有一个$p$,那必然有一个余数为$2$的位$q$,答案可以为$n-p,p+q$;如果没有,那至少有三个余数为$2$的位$p,q,r$,答案可以为$n-p-q,p+q+r$。$n%3=2$时与之类似。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
using namespace std;
typedef long long ll;
int T;
ll n,x,y;
vector<ll>a[2];
int main(){
int i;
scanf("%d",&T);
while(T--){
scanf("%lld",&n);
a[0].clear();
a[1].clear();
if(n%3==0){printf("1 %lld\n",n);continue;}
for(i=0;i<62;i++)if((1LL<<i)&n)a[i&1].push_back(1LL<<i);
if(n%3==1){
if(a[0].size()>=2){
x=n-a[0][0];
y=n-a[0][1];
}else if(a[0].size()==1){
x=n-a[0][0];
y=a[0][0]+a[1][0];
}else{
x=n-a[1][0]-a[1][1];
y=a[1][0]+a[1][1]+a[1][2];
}
}else{
if(a[1].size()>=2){
x=n-a[1][0];
y=n-a[1][1];
}else if(a[1].size()==1){
x=n-a[1][0];
y=a[0][0]+a[1][0];
}else{
x=n-a[0][0]-a[0][1];
y=a[0][0]+a[0][1]+a[0][2];
}
}
printf("2 %lld %lld\n",x,y);
assert((x|y)==n);
assert(x%3==0);
assert(y%3==0);
}
}
E
题目描述
解题思路
AC代码
2
F
题目描述
解题思路
AC代码
2
G
题目描述
解题思路
AC代码
2
H
题目描述
解题思路
AC代码
2
I
题目描述
问一个字符串中能找到最大的子串集的大小,其中满足集合中任意两个子串,其正序倒序均不相等。
解题思路
相当于将原串翻转,这样正序倒序都会出现两次,求出本质不同子串个数除以二即为答案,但回文串会被少统计,于是再加上本质不同的回文串数量。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
typedef long long ll;
using namespace std;
struct PT{
int tr[N][P],fail[N],cnt[N]/*,num[N]*/,len[N];
int tot,s[N],n,last,i;
int newnode(int l){
for(i=0;i<P;i++)tr[tot][i]=0;
cnt[tot]=0;
len[tot]=l; //num[tot]=l;
return tot++;
}
void init(){
n=last=tot=0;
newnode(0);newnode(-1);
s[0]=-1;
fail[0]=1;
}
int getfail(int p){
while(s[n-len[p]-1]!=s[n])p=fail[p];
return p;
}
void add(int p){
s[++n]=p;
int cur=getfail(last);
if(!tr[cur][p]){
int now=newnode(len[cur]+2);
fail[now]=tr[getfail(fail[cur])][p];
tr[cur][p]=now;
//num[now]=num[fail[now]]+1;
}
last=tr[cur][p];
cnt[last]++;
}
void insert(char a[]){
int i;
for(i=0;a[i];i++)add(a[i]-'a');
}
void count(){
for(i=tot-1;i>=0;i--)cnt[fail[i]]+=cnt[i];
}
}p;
struct SAM{
ll ans;
int len[N<<1],fa[N<<1],tr[N<<1][P];
int siz,last;
void init(){
last=siz=1;
fa[1]=ans=len[1]=0;
memset(tr[1],0,sizeof(tr[1]));
}
int newnode(){
++siz;
memset(tr[siz],0,sizeof(tr[siz]));
fa[siz]=len[siz]=0;
return siz;
}
void add(char c){
int s=c-'a',p=last,np=newnode();
last=np;
len[np]=len[p]+1;
while(p&&!tr[p][s])tr[p][s]=np,p=fa[p];
if(!p)fa[np]=1;
else{
int q=tr[p][s];
if(len[p]+1==len[q])fa[np]=q;
else{
int nq=newnode();
len[nq]=len[p]+1;
memcpy(tr[nq],tr[q],sizeof(tr[q]));
fa[nq]=fa[q];
fa[q]=fa[np]=nq;
while(tr[p][s]==q)tr[p][s]=nq,p=fa[p];
}
}
ans+=len[last]-len[fa[last]];
}
void insert(char a[]){
int i;
for(i=0;a[i];i++)add(a[i]);
}
}s;
char a[N];
int main(){
int i,l;
scanf("%s",a);
l=strlen(a);
p.init();p.insert(a);
a[l]='a'+26;for(i=1;i<=l;i++)a[l+i]=a[l-i];
s.init();s.insert(a);
printf("%lld",(s.ans-(l+1LL)*(l+1)+(p.tot-2))/2);
return 0;
}
J
题目描述
在一个图里求$S$到$T$的最短路,其中可以把任意$k$条边的边权置零。
解题思路
上来一看,这不一眼题,直接$dis[i][j]$表示用了$i$次置零,到$j$的最短路径长度,$dijkstra/spfa$转移时候多带一维即可。
$WAWAWA$
期间重构了无数次代码,最后一次莫名其妙$A$的也不知道怎么$A$的。
好,回头补题,检查了一下,
$nmdwsm$
那就把赛时重构了两遍的代码全发出来吧…改了$kst$之后它们全都过了……白白废了比赛时的一个小时……
AC代码-1——dijkstra+前向星
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
typedef long long ll;
using namespace std;
int n,m,k,s,t;
struct Edge{
int e,n,l;
}e[N<<1];
int hd[N],cnt;
void add(int a,int b,int l){
e[++cnt].e=b;e[cnt].n=hd[a];hd[a]=cnt;
e[cnt].l=l;
}
int dis[N][N];
struct node{
int step,nod,dis;
bool operator<(const node&a)const{
return dis>a.dis;
}
};
priority_queue<node>Q;
void dijkstra(){
int i;
memset(dis,0x3f,sizeof(dis));
Q.push({0,s,0});
dis[0][s]=0;
while(!Q.empty()){
int t=Q.top().nod,ds=Q.top().dis,st=Q.top().step;
Q.pop();
for(i=hd[t];i;i=e[i].n){
int q=e[i].e;
if(ds+e[i].l<dis[st][q]){
dis[st][q]=dis[st][t]+e[i].l;
Q.push({st,q,dis[st][q]});
}
if(st+1<=k&&ds<dis[st+1][q]){
dis[st+1][q]=dis[st][t];
Q.push({st+1,q,dis[st+1][q]});
}
}
}
}
int main(){
int i;
scanf("%d%d%d%d%d",&n,&m,&s,&t,&k);
while(m--){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
dijkstra();
int ans=1e9;
for(i=0;i<=k;i++)ans=min(ans,dis[i][t]);
printf("%d",ans);
return 0;
}
AC代码-2——SPFA+前向星
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
typedef long long ll;
using namespace std;
int n,m,K,S,T;
struct Edge{
int e,n;ll l;
}e[N<<5];
int hd[N],cnt;
void add(int a,int b,ll l){
e[++cnt].e=b;
e[cnt].n=hd[a];
e[cnt].l=l;
hd[a]=cnt;
}
ll dis[N][N];
queue<pair<int,int>>Q;
int vis[N][N];
int main(){
int i;
scanf("%d%d%d%d%d",&n,&m,&S,&T,&K);
while(m--){
int u,v;ll w;
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
memset(dis,0x3f,sizeof(dis));
while(!Q.empty())Q.pop();
Q.push(mp(S,0));
dis[S][0]=0;
while(!Q.empty()){
int u=Q.front().first,k=Q.front().second;
Q.pop();
vis[u][k]=0;
for(i=hd[u];i;i=e[i].n){
int v=e[i].e;ll w=e[i].l;
if(dis[u][k]+w<dis[v][k]){
dis[v][k]=dis[u][k]+w;
if(!vis[v][k])vis[v][k]=1,Q.push(mp(v,k));
}
if(k<K&&dis[u][k]<dis[v][k+1]){
dis[v][k+1]=dis[u][k];
if(!vis[v][k+1])vis[v][k+1]=1,Q.push(mp(v,k+1));
}
}
}
ll ans=1e15;
for(i=0;i<=K;i++)ans=min(ans,dis[T][i]);
printf("%lld\n",ans);
return 0;
}
AC代码-3——SPFA+vector
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
typedef long long ll;
using namespace std;
int n,m,K,S,T;
vector<int>G[N];
vector<ll>W[N];
void add(int a,int b,ll l){
G[a].pb(b);W[a].pb(l);
}
ll dis[N][N];
queue<pair<int,int>>Q;
int vis[N][N];
int main(){
int i;
scanf("%d%d%d%d%d",&n,&m,&S,&T,&K);
while(m--){
int u,v;ll w;
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
memset(dis,0x3f,sizeof(dis));
while(!Q.empty())Q.pop();
Q.push(mp(S,0));
dis[S][0]=0;
while(!Q.empty()){
int u=Q.front().first,k=Q.front().second;
Q.pop();
vis[u][k]=0;
for(i=0;i<(int)G[u].size();i++){
int v=G[u][i];ll w=W[u][i];
if(dis[u][k]+w<dis[v][k]){
dis[v][k]=dis[u][k]+w;
if(!vis[v][k])vis[v][k]=1,Q.push(mp(v,k));
}
if(k<K&&dis[u][k]<dis[v][k+1]){
dis[v][k+1]=dis[u][k];
if(!vis[v][k+1])vis[v][k+1]=1,Q.push(mp(v,k+1));
}
}
}
ll ans=1e15;
for(i=0;i<=K;i++)ans=min(ans,dis[T][i]);
printf("%lld\n",ans);
return 0;
}
K
题目描述
给一个大数,求其中连续子串对应数字能被$300$整除的种类数。
解题思路
考虑记录到第$i$个数字的时候,结尾为$i$的被$3$除余$0,1,2$的个数,它们与后面的两个零组成一种答案。然后再特殊处理一下未记录的单个$0$和两个$0$的情况即可。
AC代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
typedef long long ll;
using namespace std;
char a[N];
int num[3][N];
ll ans;
int main(){
int i,j;
scanf("%s",a+1);
for(i=1;a[i];i++){
int now=a[i]-'0';
for(j=0;j<3;j++){
num[((j*10)+now)%3][i]=num[j][i-1];
}
num[now%3][i]++;
if(a[i+1]=='0'&&a[i+2]=='0')ans+=num[0][i];
if(a[i]=='0')ans++;
if(a[i]=='0'&&a[i+1]=='0')ans++;
}
printf("%lld",ans);
return 0;
}