2019 BUAA Spring Training 10 题解

Solved	A	B	C	D	E
5/5	Ø	O	Ø	O	O

O for passing during the contest
Ø for passing after the contest
! for attempted but failed
· for having not attempted yet

比赛链接

A CF434E - Furukawa Nagisa’s Tree

题目描述
给一棵树，每个点有给定权值$val_i$。定义一个长度为$l$的简单路径$[u,v]$是好的当且仅当$(\sum_{i=0}^{l-1}val_ik^i)%y=x$。问有多少条路径$[u,v]$满足$[u,p][p,v][u,v]$三条路径同好坏，其中$p$为$[u,v]$上一点。

解题思路
太神了这题orz

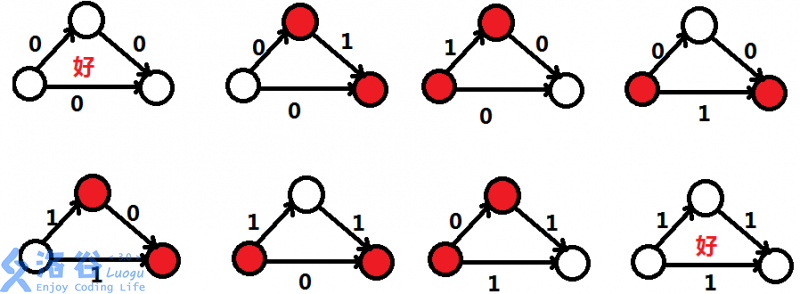
首先我们观察任意三点构成的带方向和好坏的三角形，共有八种，有两种是答案所求，这两种需要满足三条边同好坏，不是很好求得。所以我们考虑，任意一个不符合答案要求的三角形必然满足有两个点连接两条不同好坏的边，这就可以与第三边脱离关系了，可以用点分治求解。

我们假设一个点$i$作为好边终点有$in[1][i]$种，作为坏边终点有$in[0][i]$种，作为好边起点有$out[1][i]$种，作为坏边起点有$out[0][i]$种。

下面引用洛谷题解中的一张图：（转侵删）

通过对上述六种三角形的计数，与某个点$i$有关的（注意，不是上述链接中题解中所说产生的）坏三角形个数即为$\frac12(4in[1][i]in[0][i]+4out[1][i]out[0][i]+2in[1][i]out[0][i]+2out[1][i]in[0][i])$，而一个三角形里有两个这样的点，所以答案即为$n^3$减去这些数的一半。

这个式子感觉很迷惑，让我们扔掉这个很抽象的图不管，用更形象的方式去理解。

考虑一个三角形$[u,p][p,v][u,v]$，根据题目描述中的定义，显然这三个点互不等价。任意一个点$m$都必为这个三元组中的任意一个，故可以假设$m$为$u,p,v$中的某一点，则$m$的贡献（有关的坏三角形数）即为$m$分别为这三个点的贡献之和。当$m$为$u$点时，贡献为$out[1]out[0]+out[0]out[1]$（考虑$u\rightarrow p,u\rightarrow v$两条边的不同）；当$m$为$v$点时，贡献为$in[1]out[0]+in[0]out[1]$；当$m$为$u$点时，贡献为$in[1]in[0]+in[0]in[1]$。加起来即为刚才的式子。

我们回过头理解这个三角形的图，其实是对于一个点，它与另一个顶点同时产生一个坏三角形。而这个图中计数是对每一个三角形中两个顶点计数分别计了一次，故需要除以二。这里很绕，可以理解为一个顶点对应的两份”答案“其实是不能同时满足的，但是是必然满足某一个的。

而对于最后的答案，因为是枚举每一个顶点，所以一个坏三角形会被计数两次，所以需要再除以二。

说了一大串，下面进入正题。

我们要统计的是经过给定树根的路径的起点与终点的$in,out$值。

首先，在$calc$里通过$dfs$可以很容易地得出每一个子树中的节点$p$到根的$up[p]$和$down[p]$值（从该节点向根走，从根走到该节点）。一条通过$rt$的路径$[p,q]$是好的当且仅当$(up[p]-val[rt]+down[q]\times k^{depth[p]})%y=x$。化一下式子，把$p,q$分离开，有$(buc1(p)=(-up[p]+val[rt]+x)\times k^{-depth[p]}%y)=(buc2(q)=down[q]%y)$。

于是，找到所有通过$rt$的路径的$buc1,buc2$以及其对应起止点，排一下序，即可双指针线性找出每一个起止点对应的$in,out$值增量。我们发现这里重复统计了在相同子树里的不合法路径，故需要把这些东西容斥掉。

时间复杂度$O(\log n(n+n\log n))=O(n\log^2n)$。

AC代码
点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define N 100010
int n,y,k,x;
ll ans;
struct Edge{
    int e,n;
}e[N<<1];
int hd[N],cnt;
void add(int a,int b){e[++cnt].e=b;e[cnt].n=hd[a];hd[a]=cnt;}
int siz[N],mxt[N],vis[N];
int sum,rt;
int val[N],kpow[N]={1},inv[N]={1};
void getrt(int p,int f){
    int i,q;
    siz[p]=1;mxt[p]=0;
    for(i=hd[p];i;i=e[i].n){
        q=e[i].e;
        if(q==f||vis[q])continue;
        getrt(q,p);
        siz[p]+=siz[q];
        mxt[p]=max(mxt[p],siz[q]);
    }
    mxt[p]=max(mxt[p],sum-mxt[p]);
    if(mxt[p]<mxt[rt])rt=p;
}
int in[2][N],out[2][N];
pair<int,int>buc1[N],buc2[N];
int tot;
void getv(int p,int f,int dep,int up,int down){
    int i,q;
    up=((ll)up*k+val[p])%y;
    down=(down+(ll)val[p]*kpow[dep])%y;
    buc1[++tot]=make_pair((((ll)x-up+y)*inv[dep]+val[rt])%y,p);
    buc2[tot]=make_pair(down,p);
    for(i=hd[p];i;i=e[i].n){
        q=e[i].e;
        if(q==f||vis[q])continue;
        getv(q,p,dep+1,up,down);
    }
}
void calc(int p,int flag,int up,int down){//flag=1 -> depth=1 && (*-1)容斥
    int i,q;
    tot=0;
    up=((ll)up*k+val[p])%y;
    down=((ll)val[p]*kpow[flag]+down)%y;
    buc1[++tot]=make_pair((((ll)x-up+y)*inv[flag]+val[rt])%y,p);
    buc2[tot]=make_pair(down,p);
    for(i=hd[p];i;i=e[i].n){
        q=e[i].e;
        if(!vis[q])getv(q,p,1+flag,up,down);
    }
    sort(buc1+1,buc1+tot+1);
    sort(buc2+1,buc2+tot+1);
    buc1[tot+1]=make_pair(-1,-1);
    buc2[tot+1]=make_pair(-1,-1);
    int pa=1,pb=1,num=1;
    for(i=1;i<=tot;i++){
        while(pb<=tot&&buc1[i].first>buc2[pb].first)pb++;
        if(buc1[i].first!=buc2[pb].first)continue;
        while(pb<tot&&buc2[pb].first==buc2[pb+1].first)num++,pb++;
        out[1][buc1[i].second]+=(flag?-1:1)*num;
        if(i==tot||buc1[i].first!=buc1[i+1].first)num=1;
    }
    for(i=1;i<=tot;i++){
        while(pa<=tot&&buc1[pa].first<buc2[i].first)pa++;
        if(buc1[pa].first!=buc2[i].first)continue;
        while(pa<tot&&buc1[pa].first==buc1[pa+1].first)num++,pa++;
        in[1][buc2[i].second]+=(flag?-1:1)*num;
        if(i==tot||buc2[i].first!=buc2[i+1].first)num=1;
    }
}
void solve(int p){
    vis[p]=1;
    int i,q;
    calc(p,0,0,0);
    for(i=hd[p];i;i=e[i].n){
        q=e[i].e;
        if(!vis[q])calc(q,1,val[rt],val[rt]);
    }
    for(i=hd[p];i;i=e[i].n){
        q=e[i].e;
        if(vis[q])continue;
        sum=siz[q];
        mxt[rt=0]=n+1;
        getrt(q,0);
        solve(rt);
    }
}
int qp(int a,int b){
    int ans=1;
    for(;b;b>>=1,a=(ll)a*a%y)if(b&1)ans=(ll)ans*a%y;
    return ans;
}
int main(){
    int i,X,Y;
    int kinv=qp(k,y-2);
    scanf("%d%d%d%d",&n,&y,&k,&x);
    for(i=1;i<N;i++)kpow[i]=(ll)kpow[i-1]*k%y,inv[i]=(ll)inv[i-1]*kinv%y;
    for(i=1;i<=n;i++)scanf("%d",&val[i]);
    for(i=1;i<n;i++)scanf("%d%d",&X,&Y),add(Y,X),add(X,Y);
    sum=n;mxt[rt=0]=n+1;
    getrt(1,0);
    solve(rt);
    ans=(ll)n*n*n*2;
    for(i=1;i<=n;i++){
        in[0][i]=n-in[1][i];
        out[0][i]=n-out[1][i];
        ans-=2LL*in[0][i]*in[1][i]+2LL*out[0][i]*out[1][i]+(ll)in[0][i]*out[1][i]+(ll)in[1][i]*out[0][i];
    }
    printf("%I64d\n",ans/2);
    return 0;
}

B CF746G - New Roads

题目描述

构造一棵$n$节点的树，使得除了根节点外，深度为$i$的点有$a_i$个，且恰好有$k$个叶子节点。

解题思路

先把所有都看成连到主根上，然后对于每一个节点枚举应不应该把它扔到另一个节点上使得叶子数量减少即可。

AC代码

点击

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define N 200005
int n,k,mxnum[N]={1},f[N],now[N]={2};
int main(){
    int i,mx,j;
    scanf("%d%d%d",&n,&mx,&k);
    for(i=1;i<=mx;i++)scanf("%d",&mxnum[i]),mxnum[i]+=mxnum[i-1],now[i]=mxnum[i-1]+2;
    if(n-mx<k||mxnum[mx]-mxnum[mx-1]>k)return printf("-1"),0;
    int left=n-mx-k;
    f[2]=1;
    for(i=1;i<mx;i++)f[mxnum[i]+1]=mxnum[i-1]+1;
    for(i=1;i<=mx;i++){
        for(j=mxnum[i-1]+2;j<=mxnum[i];j++){
            if(left&&now[i-1]<=mxnum[i-1])f[j]=now[i-1]++,left--;
            else f[j]=f[j-1];
        }
    }
    if(left)return printf("-1"),0;
    printf("%d\n",n);
    for(i=2;i<=n;i++)printf("%d %d\n",i,f[i]);
    return 0;
}

C CF665F - Four Divisors

题目描述
求出所有小于等于$n\leq 10^{11}$的、只有四个因数的正整数的个数。

解题思路
令$S(n,p)$为埃氏筛完第$p$个素数后，前$n$项里没被筛掉的数之和，这些数或者是质数，或者是最小质因数大于$p$的整数。

则$S(n,p)=S(n,p-1)-\sum_{2\leq k\leq n}[k的最小质因数为prime[p]]$
$=S(n,p-1)-\sum_{2\leq t\leq \lfloor \frac n{prime[p]}\rfloor}[t的最小质因数\geq prime[p]]$
$=S(n,p-1)-(S(\lfloor \frac n{prime[p]}\rfloor ,min(p-1,\sqrt{\frac n{prime[p]}})-(p-1))$

求出每一个数对应小于等于它的最大质数下标，小数据记忆化搜索，大数据暴力递归即可得出结果。

时间复杂度$O(不会算)=O(能过)$。

AC代码
点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define N 1000002
int f[N][110];
int prime[N],a[N]={1,1},cnt,mxp[N];
void initprime(){
    int i,j;
    for(i=2;i<N;i++){
        if(!a[i])prime[++cnt]=i;
        for(j=1;j<=cnt&&i*prime[j]<N;j++){
            a[prime[j]*i]=1;
            if(prime[j]%i==0)break;
        }
    }
    for(i=1;i<N;i++)mxp[i]=mxp[i-1]+!a[i];
}
ll s(ll n,int p){
    if(n<N&&p<110&&f[n][p])return f[n][p];
    ll ans;
    if(p<=0)ans=n-1;
    else ans=s(n,mxp[prime[p]-1])-s(n/prime[p],min(p-1,mxp[(int)sqrt(n/prime[p])]))+p-1;
    if(n<N&&p<110)f[n][p]=ans;
    return ans;
}
int main(){
    int i;ll n,ans=0;
    initprime();
    scanf("%I64d",&n);
    for(i=2;(ll)i*i*i<=n;i++)if(!a[i])ans++;
    for(i=1;i<=cnt;i++){
        if(((ll)prime[i]*prime[i]>=n))break;
        ans+=s(n/prime[i],mxp[(int)sqrt(n/prime[i])])-i;
    }
    printf("%I64d",ans);
    return 0;
}

D HDU3032 - Nim or not Nim?

题目描述

可以分裂的$Nim$

解题思路

爆搜一边$SG$发现有规律，直接解决即可。

AC代码

点击

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
int f(int x){
    if(x%4==1||x%4==2)return x;
    if(x%4==3)return x+1;
    return x-1;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int ans=0,a,n,i;
        scanf("%d",&n);
        for(i=0;i<n;i++)scanf("%d",&a),ans^=f(a);
        printf("%s\n",ans?"Alice":"Bob");
    }
}
/*
#define N 1000
int sg[N],vis[N];
int main(){
	int i,j;
	sg[0]=0;sg[1]=1;
	for(i=2;i<N;i++){
		memset(vis,0,sizeof(vis));
		for(j=0;j<i;j++)vis[sg[j]]=vis[sg[j]^sg[i-j]]=1;
		for(j=0;j<N;j++)if(!vis[j])break;
		sg[i]=j;
	}
	for(i=0;i<N;i++)printf("%d ",sg[i]);
	return 0;
}
*/

E ZJOI2014 - 诸神眷顾的幻想乡

题目描述

一棵树的每个节点有一个颜色$c$，且这棵树的叶子结点不超过$20$个，求这棵树两点之间颜色构成的路径不同序列个数。

解题思路

广义后缀自动机，对每一个叶子爆搜即可。对于每一个等价类$p$，其对应的不同子串个数为$maxlen(p)-minlen(p)+1$，其中$maxlen(p)$为$len_p$，$minlen(p)$为$len_{fa_p}+1$。

AC代码

点击

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define N 4000010
#define P 11
struct Edge{int e,n;}e[N<<1];
int hd[N],cnt,deg[N];
void add(int a,int b){e[++cnt].e=b;e[cnt].n=hd[a];hd[a]=cnt;}
struct ExtendedSAM{
    int len[N],fa[N],tr[N][P];
    int siz;
    void init(){
        int i;
        siz=1;len[0]=-1;
        for(i=0;i<P;i++)tr[0][i]=1;
    }
    int insert(int s,int p){
        int np=++siz;
        len[np]=len[p]+1;
        while(!tr[p][s])tr[p][s]=np,p=fa[p];
        int q=tr[p][s];
        if(len[p]+1==len[q])fa[np]=q;
        else{
            int nq=++siz;
            len[nq]=len[p]+1;
            fa[nq]=fa[q];
            fa[q]=fa[np]=nq;
            memcpy(tr[nq],tr[q],sizeof(tr[q]));
            while(tr[p][s]==q)tr[p][s]=nq,p=fa[p];
        }
        return np;
    }
}sam;
int a[N],n,c;
void dfs(int now,int f,int pos){
    int i,nxt=sam.insert(a[now],pos);
    for(i=hd[now];i;i=e[i].n){
        int q=e[i].e;
        if(q!=f)dfs(q,now,nxt);
    }
}
int main(){
    int i,u,v;
    sam.init();
    scanf("%d%d",&n,&c);
    for(i=1;i<=n;i++)scanf("%d",&a[i]);
    for(i=1;i<n;i++)
        scanf("%d%d",&u,&v),
        add(u,v),add(v,u),
        deg[u]++,deg[v]++;
    for(i=1;i<=n;i++)if(deg[i]==1)dfs(i,0,1);
    ll ans=0;
    for(i=2;i<=sam.siz;i++)ans+=sam.len[i]-sam.len[sam.fa[i]];
    printf("%lld",ans);
    return 0;
}